MATLAB实现数字PID控制器的仿真分析

"该文档是关于数字PID控制器的计算机仿真的学习资料，主要涉及计算机控制技术课程中的PID控制器设计和参数整定。通过MATLAB软件进行仿真，针对三种不同的被控对象（二阶振荡环节、非最小相位特性的过程、具有低通特性和纯滞后的过程）进行控制，目标是确定最佳PID参数，使得系统性能满足特定要求。" 本文档详细阐述了数字PID控制器的计算机仿真过程，旨在帮助学习者深入理解PID控制器的工作原理和参数设定。PID控制器由比例(P)、积分(I)和微分(D)三个部分组成，其基本算法如下： △u(k) = q0 * e(k) + q1 * e(k-1) + q2 * e(k-2) u(k) = u(k-1) + △u(k) 这里的e(k)是误差信号，q0、q1、q2分别是比例、积分和微分增益，而u(k)是控制输出。初始条件设定为：u(k-1)=u(k-2)=0，e(k-1)=e(k-2)=0，y(k-1)=y(k-2)=0。 在仿真中，选择了三种典型的被控对象： 1. 二阶振荡环节：G(z) = (1 / (bz1 + bz2)) / (1 + az1 + az2)，参数分别为a、b和T。 2. 具有非最小相位特性的过程：G(z) = (1 / (bz1 + bz2)) / (1 + az1 + az2^2)，具有负实部的极点。 3. 具有低通特性和纯滞后的过程：G(z) = (bz1 + bz2 + bz3) / (z^d * (1 + az1 + az2 + az3))，包含了延迟项d。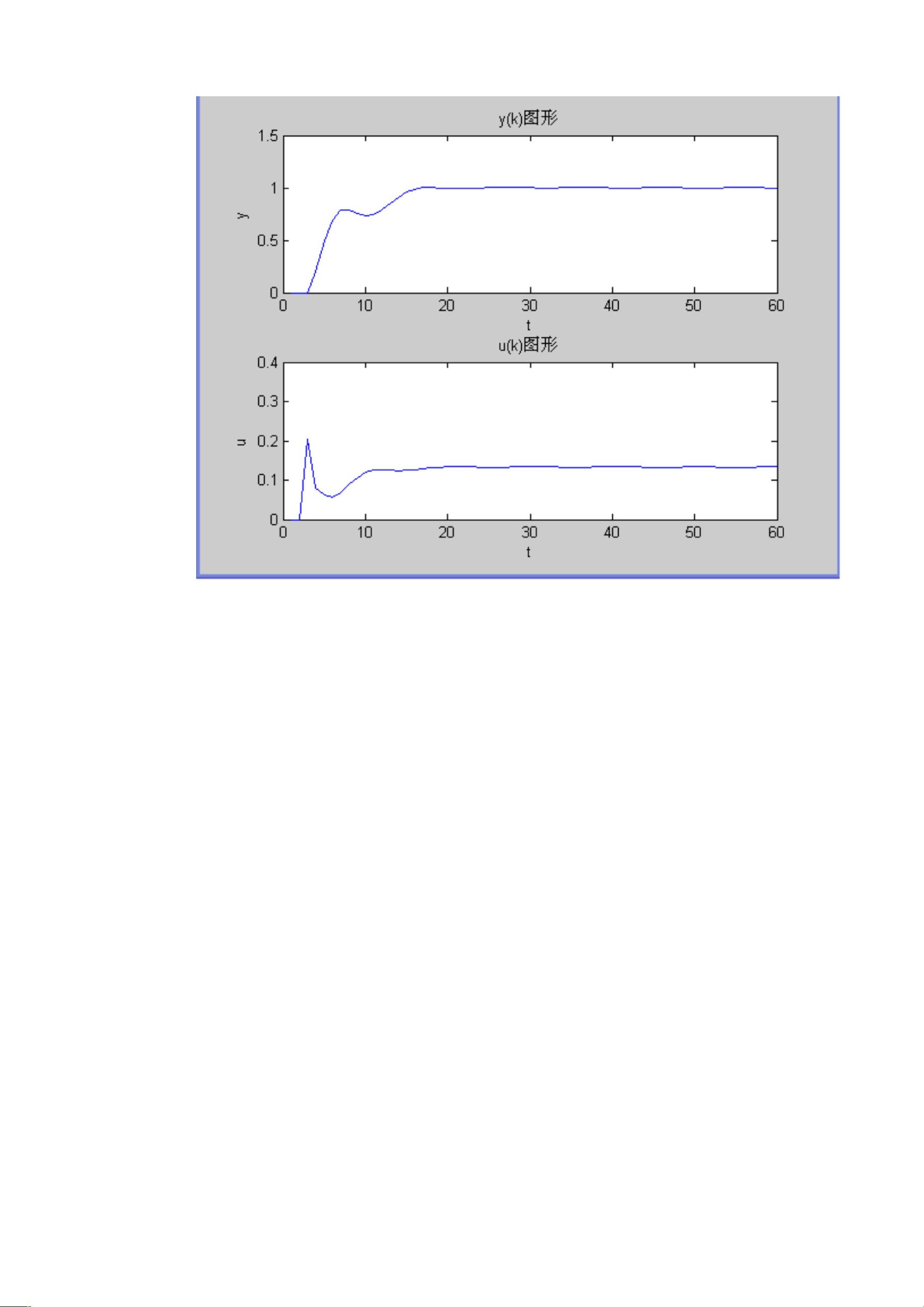 仿真要求包括： 1. 使用MATLAB计算超过40个时间步长的y(k)和u(k)，并绘制相关曲线。 2. 对这三种对象，当采样时间T为1或2秒时，通过整定找到最佳的PID参数。 3. 整定方法采用凑试法，需要计算上升时间(tr)、超调量(poss)和收敛时间(ts)，并确保poss<5%，tr<25，ts<40。 整定过程举例： 对于二阶振荡环节，首先设置不确定的Kp、Ti和Td值，然后根据PID公式计算q0、q1和q2。接着，通过MATLAB编写程序，初始化误差e、控制输入u和系统输出y的矩阵，以及计算增量du。在仿真过程中，不断调整PID参数，直至系统性能指标满足要求。 通过对这三种被控对象的仿真，学习者可以深入掌握PID控制器的参数整定方法，理解不同系统特性的控制策略，并熟悉MATLAB在控制系统仿真的应用。这个过程有助于培养实际工程中的问题解决能力。