4394 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 14, NO. 8, AUGUST 2015
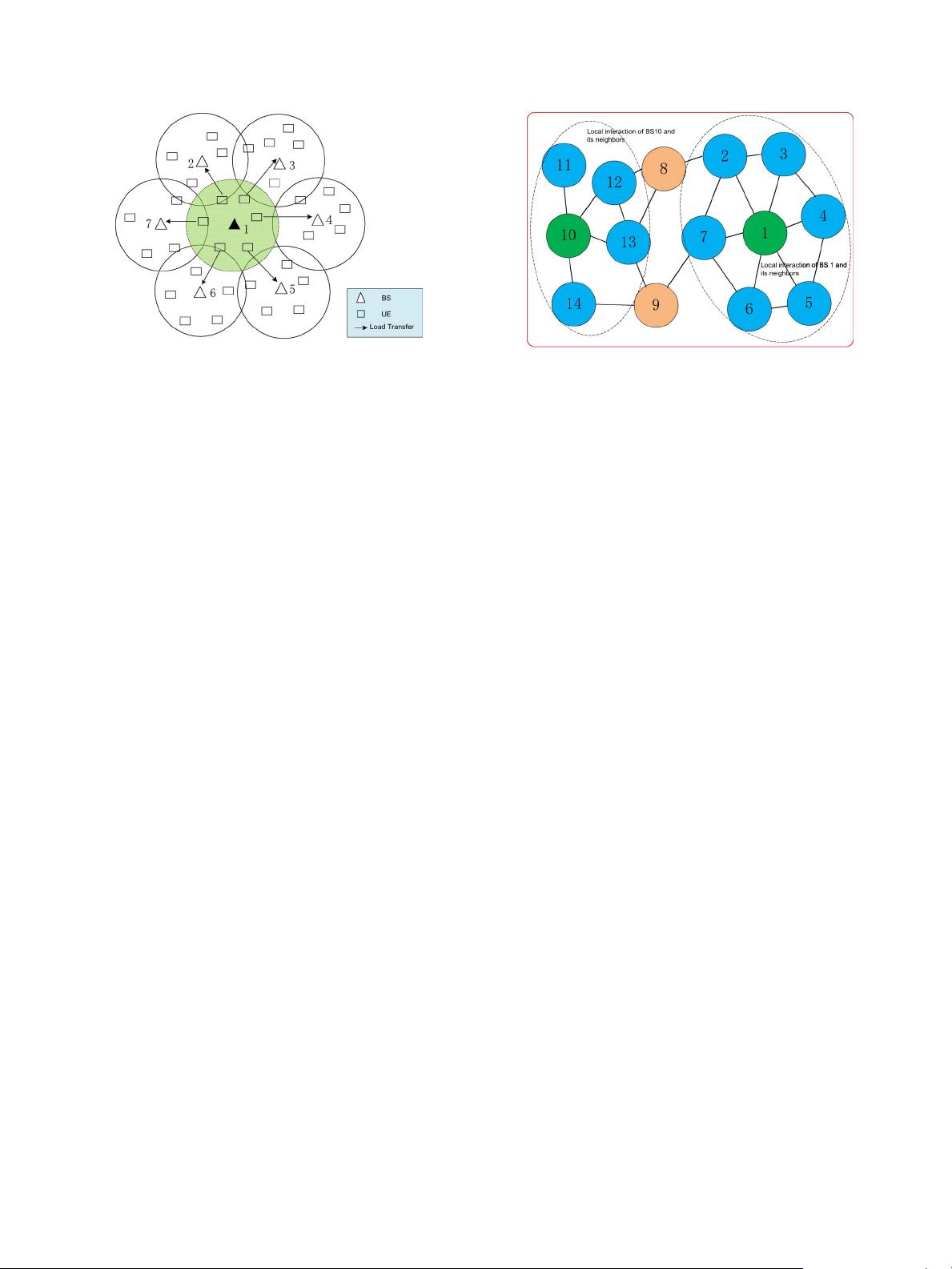
Fig. 1. BS cooperation for energy saving.
especially when the number of BSs is large; Second, it needs a
centralized controller which collects the channel state informa-
tion and traffic load information from all BSs in practice.
It is worth noting that the existing works [4], [16] only pro-
pose some greedy heuristic algorithms to find a feasible solu-
tion to the problem (6), and there is no theoretic analysis on the
optimality property. Moreover, the proposed algorithms require
the information from all involved BSs. Then, Oh et al. [18] aims
to reduce the information exchange by designing distributed
algorithms. However, no optimality of the algorithm can be
guaranteed.
III. L
OCAL COOPERATION GAME FOR
ENERGY-SAV I N G BS SWITCHING
In this section, we discuss on the distributed optimization of
the above problem (6) by using game theory [35]–[43], which is
a powerful tool to analyze the interactions between distributed
decision makers and thereby improve the performance of de-
centralized networking/framework.
A. Local Interaction and Cooperative BS Sleeping Mechanism
When one BS is turned off, apparently, this would result
in an increase in the system load of neighboring BSs. This is
because those UEs originally associated with the switched-off
BS need to be transferred to its neighbors (as shown in Fig. 1),
even they may experience lower service rates R
k
(x, B
on
) due
to farther distances between the UEs and their new serving
BSs. The neighboring BSs (BSs 2-7) are serving as acceptors
for BS 1 by cooperatively sharing its traffic (as shown by the
arrows) and allowing BS 1 to turn into sleeping mode for saving
energy. At the same time, for supporting the extended coverage
zones, transmission power of these acceptors (BSs 2-7) should
be adjusted.
The network model is presented in Fig. 2 to capture the local
interaction among the neighboring BSs. The solid lines between
any two BSs denote the interaction between them. When BS 1
and BS 10 are switched off, the local interaction domain of BS 1
and BS 10 are illustrated by the dashed lines. For instance, as
described in the figure, BS 10 and its neighboring BSs 11-14
are interacting via their own local processes. Here, BS 10 may
have no knowledge on the behavior of other BSs beyond its own
Fig. 2. Distributed network model.
domain (i.e., BSs 1-9). However, the neighboring BSs of BS 10
are also interacting with their respective neighboring BSs, and
thus, BS 10 is directly and indirectly influencing the behavior
of all the other BSs in the system. In turn, local behaviors of
the BSs would generate the global behavioral pattern of the
whole system. This type of interaction f ollows the principle of
ecological self-organization [27]–[29].
Definition 1: An Interaction Graph is defined by G
r
=
(K,ε), where K is the set of vertices (BSs as players), ε is the
set of edges. We say BSs j and k are direct neighbors if they are
connected by an edge, i.e., (j, k) ∈ ε. Moreover, we define C
k
as the set of BS k’s neighbors, C
k
= {j :(j, k) ∈ ε}. Notably,
j ∈C
k
⇔ k ∈C
j
.
B. Graphical Game Model
Then, the graphical game model is formally denoted by G =
[G
r
, {S
k
}
k∈K
, {U
k
}
k∈K
, {f
k
}
k∈K
], where S
k
= {0, 1} (0 de-
notes “off”, 1 denotes “on”) is the set of available switching
strategy for player (BS) k, U
k
is the utility function of player
k to evaluate the energy consumption, and f
k
represents a
correspondence function for satisfaction of the constraint [32].
An strategy profile of all the players is a vector, denoted by s =
(s
1
,s
2
,...,s
K
) ∈S, where S = S
1
⊗S
2
⊗···⊗S
K
repre-
sents the joint strategy space for all the players. Besides, the
strategy profile of all the players excluding k is denoted by
s
−k
=(s
1
,...,s
k−1
,s
k+1
...,s
K
) ∈S
−k
, where S
−k
= S
1
⊗
···⊗S
k−1
⊗S
k+1
⊗···⊗S
K
. Additionally, the strategy pro-
file of player k’s neighbors is denoted by s
C
k
∈S
C
k
, where
S
C
k
= ⊗
j∈C
k
S
j
represents the joint strategy space for player
k’s direct neighbors.
Based on the interaction graph, the energy consumption of
each player (say player k) only depends on the strategies of
itself and its neighbors, and thus can be denoted by φ
k
(s
k
, s
C
k
).
Moreover, because 1) the neighboring BSs connected though
high-speed wireline can easily communicate with each other
(e.g., over X2 interface in LTE), 2) efficiency of the game can
be greatly improved by local cooperation, we design the utility
function as
U
k
(s
k
, s
D
k
)=−
φ
k
(s
k
, s
C
k
)+
i∈C
k
φ
i
(s
i
, s
C
i
)
, (7)




















