数字信号处理指南：快速傅里叶变换详解

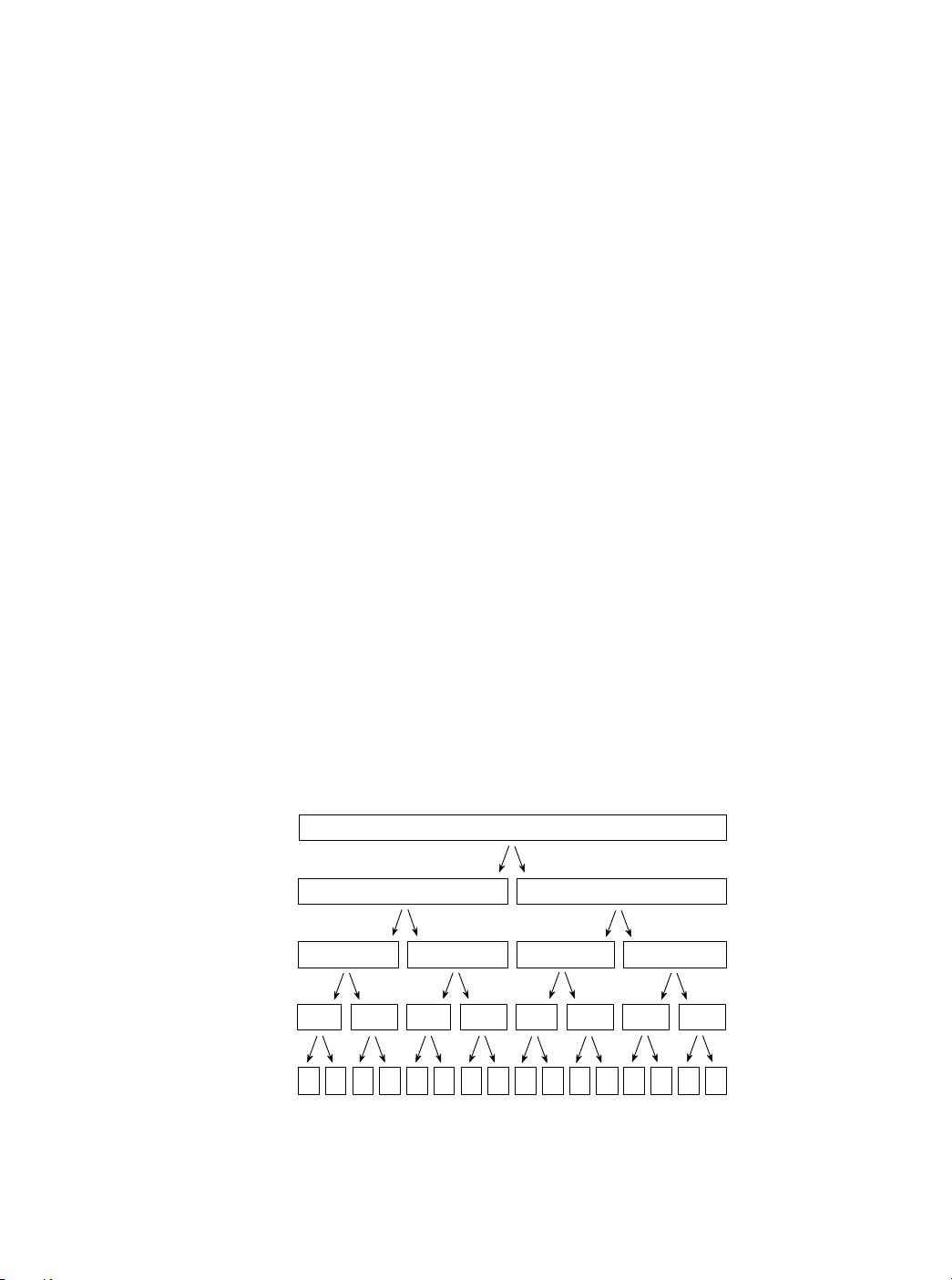
"《科学家与工程师的数字信号处理指南-12》涵盖了快速傅里叶变换（FFT）在计算离散傅里叶变换（DFT）中的应用，该方法极大地提高了计算效率，使得许多信号处理技术变得实际可行。尽管FFT算法复杂，但已有现成的代码库可供使用，即使不完全理解其内部工作原理，也能轻松应用。" 在数字信号处理（DSP）领域，快速傅里叶变换（FFT）是一个至关重要的工具。它是一种高效计算离散傅里叶变换（DFT）的方法，与解线性方程组或使用相关方法相比，FFT能够显著减少计算时间，提高了数百倍的效率。这种提升就像从步行变为乘坐喷气式飞机旅行一样显著。如果没有FFT，许多现代信号处理技术将无法实施，因为它们依赖于快速、准确的频域分析。 FFT算法的发明归功于J.W. Cooley和J.W. Tukey，他们在1965年发表的论文中介绍了这一方法，但其实该技术在此之前已被其他人发现。例如，德国数学家和其他研究者早些年就已经探讨过类似的技术。FFT的核心在于它的分治策略，将大问题分解为小问题进行解决，然后将结果组合，从而大幅减少了所需的乘法和加法操作。 尽管FFT算法的实现相当复杂，通常需要几十行代码，但它已经成为标准的库函数，可以方便地集成到各种软件和硬件系统中。对于大多数用户来说，理解如何使用这些预编译的FFT函数比深入理解其内部工作机制更为重要。通常，开发者只需要调用相应的函数，提供输入数据和选择合适的参数，就能得到DFT的结果。 在实际应用中，FFT常用于音频分析、图像处理、通信系统、频谱分析以及滤波设计等多个领域。例如，在音频处理中，FFT可以用来分析声音信号的频率成分，帮助我们理解音乐或语音的基本构成。而在通信系统中，FFT可以用于频谱监测，检测和解码传输的信号。 FFT是数字信号处理领域的基石，它的高效性使得复杂的频域分析变得切实可行，推动了科技的快速发展。无论是科研还是工程实践，理解和应用FFT都是不可或缺的技能。