解非线性Sine-Gordon方程的权重隐式差分法

"这篇论文提出了一种用于求解非线性Sine-Gordon方程的新通用差分格式，由杨晓忠和郭娜撰写，属于首发论文。文章中，作者们探讨了一类非线性Sine-Gordon方程，并介绍了一种数值解法。他们通过引入参数θ，构建了（1+1）维和广义非线性Sine-Gordon方程的加权隐式差分格式，以及（2+1）维非线性Sine-Gordon方程的ADI（Alternating Direction Implicit）差分方案。利用傅里叶分析对这些差分格式的计算稳定性进行了分析，并通过数值实验验证了方法的可行性和精确性。关键词包括非线性Sine-Gordon方程、通用差分格式、计算稳定性和数值实验。" 非线性Sine-Gordon方程是理论物理中的一个重要模型，特别是在相对论量子力学和场论中有广泛应用。解决这类方程通常需要复杂的数值方法，因为它们在数学上是高度非线性的，不容易找到解析解。在这篇论文中，作者提出了一种新的数值方法，即加权隐式差分格式，这种方法通过引入一个参数θ来改进传统方法，使其能更有效地处理（1+1）维和广义非线性Sine-Gordon方程。 对于更高维度的（2+1）维非线性Sine-Gordon方程，作者采用了ADI差分方案。ADI方法是一种处理偏微分方程的常用技术，特别适合于解决多维问题，因为它可以将原本难以处理的高维问题转化为一系列一维问题，从而降低计算复杂性。ADI方法的核心思想是通过交替求解不同方向的差分方程来实现离散化的隐式时间步进。 论文还对提出的差分格式进行了计算稳定性分析，这是评估数值方法可靠性的重要步骤。通过傅里叶分析，可以研究当扰动以不同频率和振幅存在时，数值解如何随时间变化，从而确保在一定条件下数值解能够保持稳定。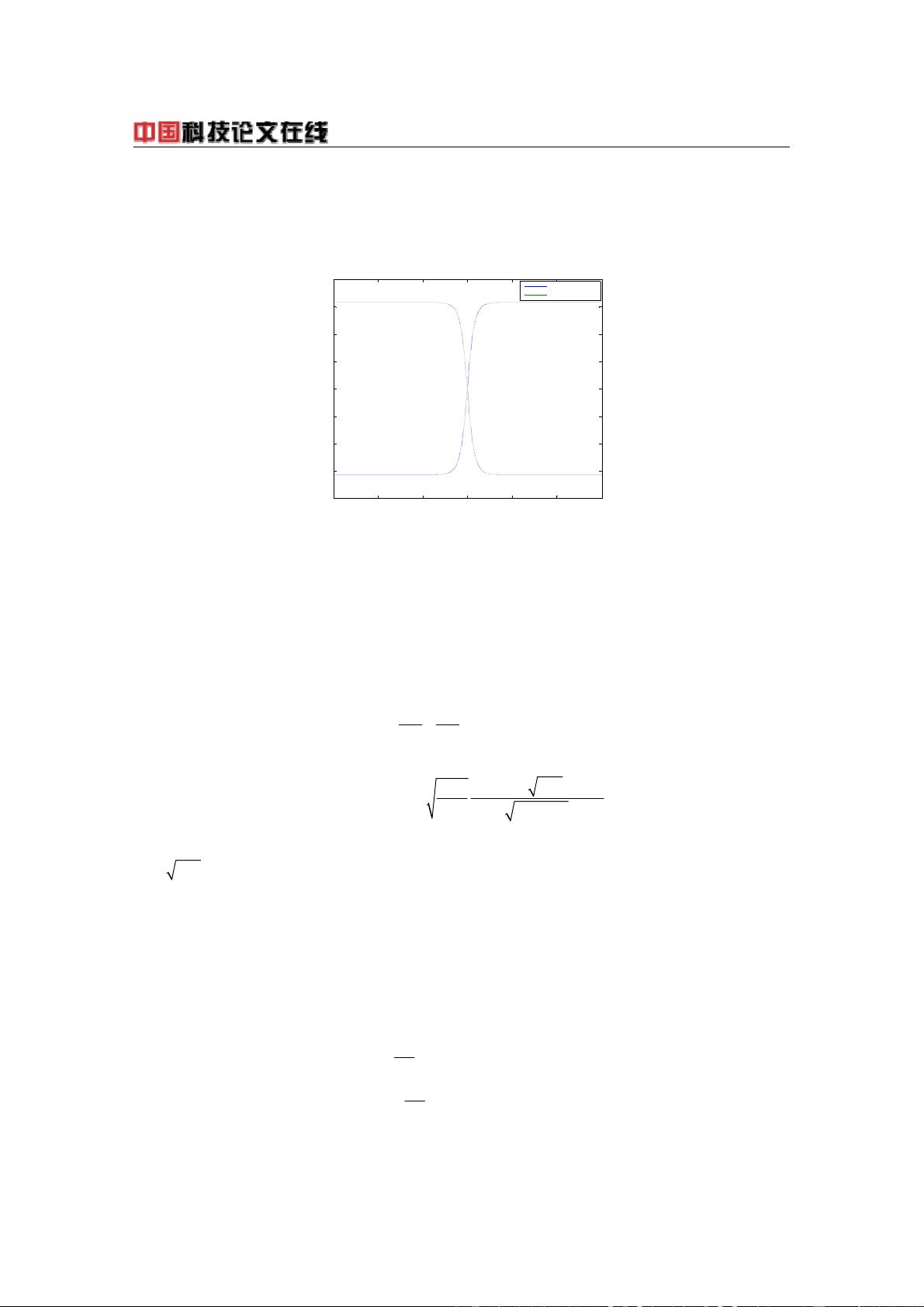 最后，作者通过数值实验展示了这些差分格式的有效性和精度。数值实验通常是验证理论方法的实际应用，通过比较模拟结果与已知解或观察到的现象，可以证明所提方法的准确性和实用性。 这篇论文为非线性Sine-Gordon方程的数值求解提供了一种新的工具，对于理论物理和工程领域的研究人员来说具有重要的参考价值。它不仅扩展了现有解法的适用范围，而且通过严谨的稳定性分析和数值验证，保证了方法的可靠性。