深入理解与实现FFT：从傅立叶变换到程序编写

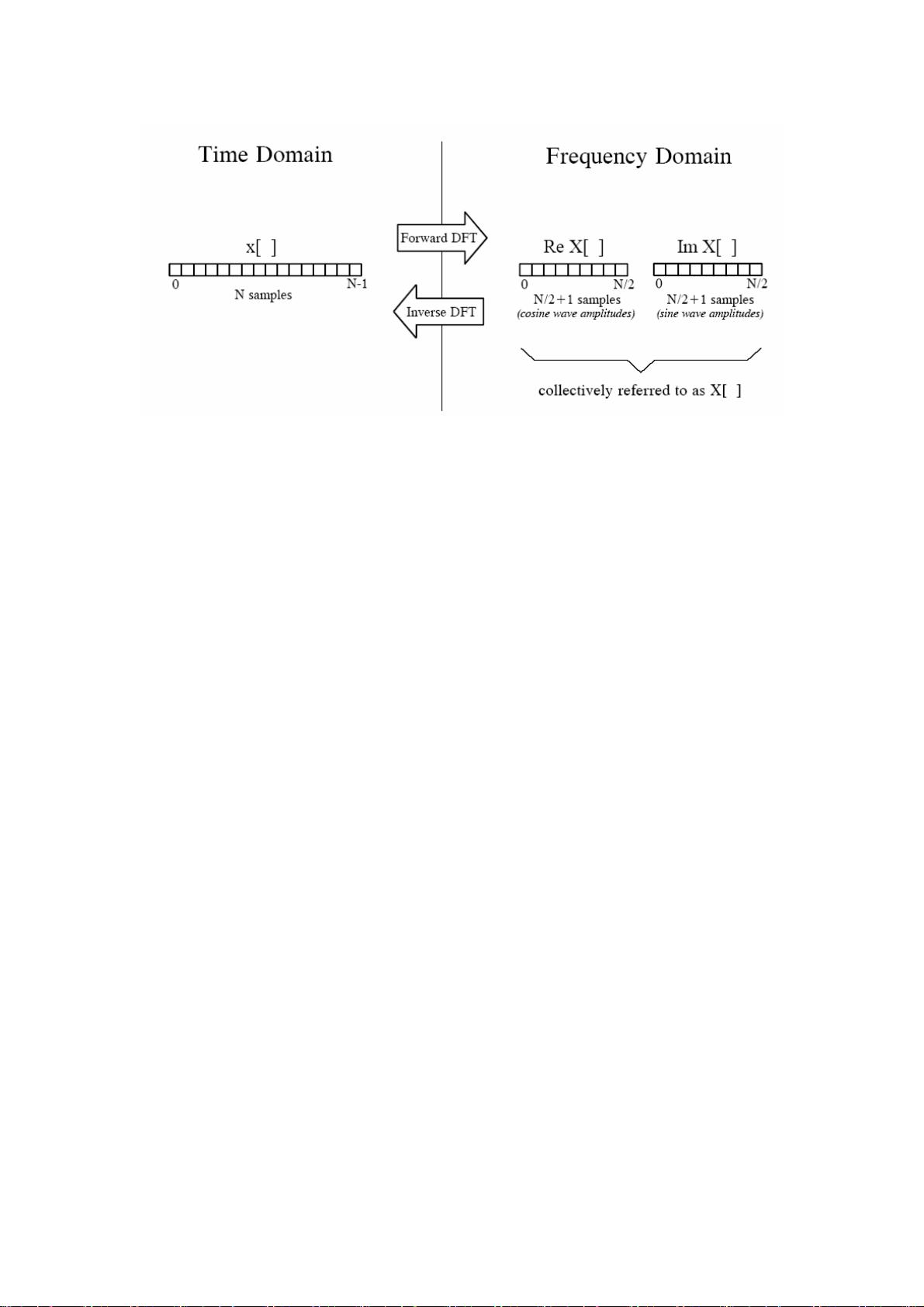
"这篇文章主要介绍了离散傅立叶变换（FFT）的背景和理解方法，作者分享了如何从感性上理解傅立叶变换，并推荐了一本由Steven W. Smith撰写的数字信号处理电子书。文章指出，傅立叶变换是由法国数学家和物理学家Fourier提出的，其理论是任何连续周期信号都可以表示为一组正弦曲线的组合。尽管最初受到拉格朗日的质疑，但后来这一理论得到了广泛接受和应用。在实际应用中，我们通常使用离散傅立叶变换（DFT）来处理数字信号，而FFT是一种更高效的计算DFT的方法。" 本文首先简述了傅立叶变换的历史，它源于Fourier对热传递的研究，他在1807年的论文中提出了任何连续周期信号都可以用正弦曲线的组合来表示，尽管这一观点最初并未得到广泛认可。随着数学和物理学的发展，傅立叶变换成为了分析和理解周期性信号的基础工具。 离散傅立叶变换（DFT）是傅立叶变换在离散时间信号上的应用，它是将一个有限长度的离散序列转换到频率域的数学工具。在数字信号处理领域，DFT广泛用于频谱分析、滤波器设计以及图像处理等。然而，直接计算DFT的复杂度是O(N^2)，对于大数据量的处理效率较低。 快速傅立叶变换（FFT）算法解决了这一问题，它将DFT的计算复杂度降低到了O(N log N)，极大地提高了计算效率。FFT算法基于分治策略，通过拆分序列、对称性质和复共轭来减少计算量。FFT的实现有多种版本，如Cooley-Tukey算法、Radix-2 FFT、Split-Radix FFT等，每种都有其适用的特定场景和优化手段。 在编程实现FFT时，需要理解基本的复数运算和DFT的数学定义，然后选择合适的FFT算法进行编程。通常，这包括初始化、递归分解、复数乘法和加法等步骤。编程实现FFT需要注意数据排列、位反转以及对复数的正确处理。 此外，理解离散傅立叶变换的物理意义和性质也很关键，例如频谱的对称性、幅度与相位的关系，以及如何从频域结果反变换回时域信号。在实际应用中，还可能涉及到窗函数的使用以减小栅栏效应，或者进行零填充以提高分辨率。 编写FFT程序不仅需要扎实的数学基础，还需要对信号处理的基本概念有深入理解。通过学习Steven W. Smith的电子书或其他相关资料，可以更好地掌握这些知识，从而成功地编写出自己的FFT程序。