which is used to supplement the missing entries in MISIM. Specifi
cally,
mGS
𝑖,𝑗
is calculated by follows
mGS
𝑖,
=exp
−𝜃
m
‖
𝐓
𝑖,:
−𝐓
,:
‖
2
(2)
where 𝐓
𝑖,:
represents the 𝑖-row in the adjacent matrix 𝐓 and 𝜃
is the
kernel bandwidth parameter which is calculated by the following formula
𝜃
=
1
𝑚
‖
𝐓
𝑖,:
‖
(3)
where 𝑚 is the number of miRNAs i.e., the row number of 𝐓.
With
MS
𝑖,𝑗
, the miRNA functional similarity matrix is denoted by
𝐀
∈ℝ
𝑚×𝑚
and constructed by
𝐀
=MS
𝑖,𝑗
.
2.3 Disease-disease Similarity
The MeSH database (http://www.ncbi.nlm.nih.gov/) is available for
studying the relationship between different diseases. We obtained a hier-
archical directed acyclic graph (DAG) directly from MeSH, where each
node represents a disease and each directed edge in the DAG is from a
general disease term to a specific disease term.
The semantic similarity scores between different diseases were calcu-
lated based on disease DAG. First, let 𝑖∈D be a disease. dag
𝑖
indicates
the node set, including node 𝑖 and its ancestor nodes in the disease DAG.
Then, the first semantic contribution of a disease 𝑡∈D to the disease 𝑖 is
denoted by
SC
𝑖,
𝑡
and
can be formulated using the following equations
(Chen et al., 2018a),
SC
1
𝑖,𝑡
=1 𝑖𝑓𝑡=𝑖
SC
1
𝑖,𝑡
=max
𝛾 SC
1
𝑖,𝑡
|
𝑡
∈𝑐ℎ𝑖𝑙𝑑𝑟𝑒𝑛 𝑜𝑓 𝑡
𝑖𝑓 𝑡𝑖
(4)
where 𝛾 is a semantic contribution decay factor, which shows that as the
distances between disease 𝑡 and its ancestor diseases increases, their con-
tribution to the semantic value of disease 𝑑 progressively decreases. 𝛾 was
set as 0.5 according to previous literature (Wang et al.,2010).
Based on the definition of semantic contribution in Eq (4), the first
semantic similarity scores between different diseases, denoted by dS
was
established. Let 𝑖,𝑗 be two different diseases. dS
𝑖,𝑗
is defined as fol-
lows.
dS
𝑖,
=
SC
1
𝑖,𝑡
+ SC
1
,𝑡
∈∩
SC
1
𝑖,𝑡
𝑡∈
+
SC
1
,𝑡
𝑡∈dag
(5)
Intuitively, dS
𝑖,𝑗
is higher if the larger part of DAG is shared by i and
j.
However, dS
ignores the significance of different disease contribu-
tions. Supposing that 𝑖,𝑡,𝑞∈ D, if disease 𝑡 only appears in the dag
𝑖
,
and 𝑞 appears in both dag
𝑖
and the dag of other diseases, 𝑡 might have
higher semantic contribution to 𝑖 than 𝑞. Thus, the second semantic con-
tribution score SC
𝑖,𝑡
was presented as follows:
SC
𝑖,𝑡
=−log
the number of dags including 𝑡
the number of disease
(6)
Based on SC
𝑖,𝑡
, the second semantic similarity score dS
, between two
diseases was presented as follows (Chen et al., 2018a)
dS
𝑖,
=
SC
2
𝑖,𝑡
+ SC
2
,𝑡
∈∩
SC
2
𝑖,𝑡
𝑡∈
+
SC
2
,𝑡
𝑡∈dag
(7)
As disease similarity measures calculated using dS
and dS
are both
from the MeSH database, it provides only a part of the entries in diseases
semantic similarity matrix. Hence, the Gaussian interaction profile kernel
similarity was adopted to complement the remaining disease similarity en-
tries.
Specifically, let 𝐓∈
0,1
×
be the adjacent matrix constructed us-
ing the known HMDD v2.0 miRNA-disease association data. 𝐓
:,𝑗
is the
𝑗-column binary vector representing disease 𝑗. Then, Gaussian interaction
profile kernel similarity between disease 𝑖 and disease 𝑗 is defined as
dGS
𝑖,
=exp
−𝜃
‖
𝐓
:,𝑖
−𝐓
:,
‖
(8)
where 𝜃
is the kernel bandwidth parameter calculated using the follow-
ing formula
𝜃
=
1
𝑛
‖
𝐓
:,
‖
(9)
where 𝑛 is the number of diseases i.e., the column number of 𝐓.
With dS
, dS
,
and dGS, the disease semantic similarity matrix is de-
noted by
𝐀
∈ℝ
𝑛×𝑛
and constructed using
𝐀
=
dS
1
𝑖,
+dS
2
𝑖,
2
,if𝑖and
has semantic similarity score
dGS
𝑖,
, otherwise
(10)
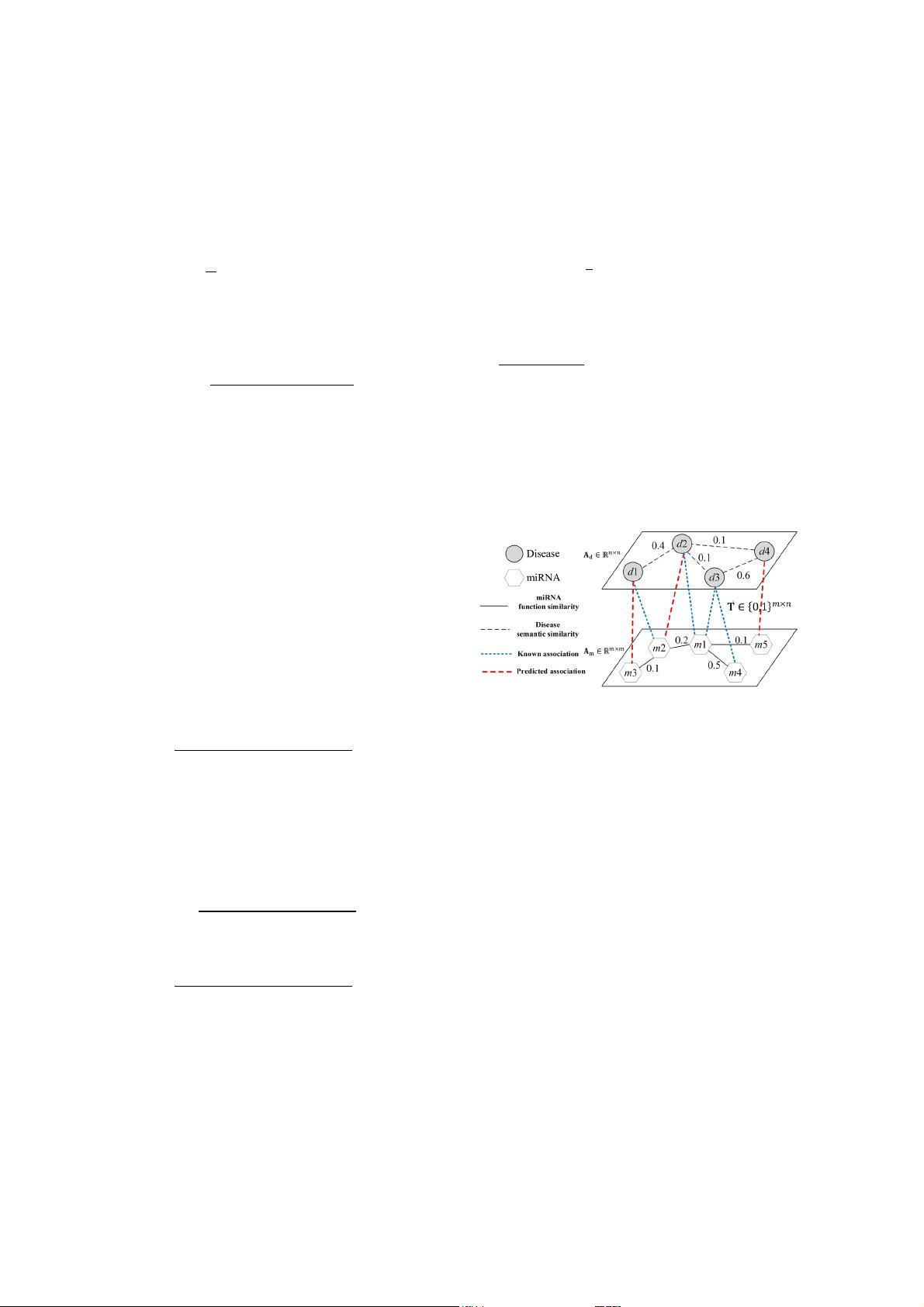
2.4 miRNA-disease Heterogeneous Information Network
We combined the miRNA functional similarity network 𝐀
, disease
semantic similarity network 𝐀
, and experimentally valid miRNA-disease
interactions
𝐓
to obtain the whole miRNA-disease heterogeneous infor-
mation network as illustrated by the Fig.1. Note that both the miRNA
functional similarity network and the disease semantic similarity network
are edge-weighted graphs.
3 Methods
In this study, based on the miRNA-miRNA similarity network, the dis-
ease-disease similarity network, and the experimentally verified miRNA-
disease data, a novel NIMCGCN method was presented to effectively
solve the problem related to the prediction of miRNA-disease association.
3.1 Matrix Completion and Inductive Matrix Completion
A problem of miRNA-disease association prediction can be consid-
ered with 𝑚 miRNAs and 𝑛 diseases, and 𝑚×𝑛 experimentally verified
miRNA-disease association matrix 𝐓∈
0,1
×
. 𝐓
𝑖,𝑗
=1 if a miRNA
𝑖 is associated with a disease 𝑗. 𝐓
𝑖,𝑗
=0 if the association between 𝑖
and 𝑗 is unknown or unobserved. Without loss of generality, Ω and Ω
were
used to denote the set of observed and unobserved or unknown miRNA-
disease entries from the known association matrix 𝐓. The observation Ω
consisted only of positive associations, i.e., if ∀
𝑖,𝑗
∈Ω, 𝐓
𝑖,𝑗
=1. Ω
is the set of unknown or unobserved entries if ∀
𝑖,𝑗
∈Ω
, 𝐓
𝑖,𝑗
=0. A
sample of observed entries Ω from a true underlying matrix 𝐐 was consid-
ered. The objective was to estimate missing entries under some additional
assumptions on the structure of the association matrix 𝐓. The most com-
mon assumption is that 𝐐 is low-rank, i.e., 𝐐=𝐅𝐆
,where 𝐅∈ℝ
×
and
𝐆∈ℝ
×
are of rank 𝑘≪𝑚,𝑛. With these notations, the basic MDA can
be formulated as the following matrix completion problems:
Fig. 1. An Illustration of a miRNAs-diseases heterogeneous infor-
mation network









