IEEE低通滤波FSPLL:三相系统正序快速检测与抗谐波设计
需积分: 11 198 浏览量
更新于2024-09-07
1
收藏 2.02MB PDF 举报
本文主要探讨了IEEE低通滤波经典应用在电力电子领域的创新设计——滤波序列相锁定环路（Filtered-Sequence Phase-Locked Loop, FSPLL）。FSPLL旨在精确检测三相系统中的正序分量，特别是在电力网格存在不平衡或谐波时提供稳定性能。论文的核心技术是结合了帕克变换(Park Transformation)和移动平均滤波器(Moving Average Filter, MAF)。
MAF在文章中被深入分析，通过数学建模，其性能在Bode图中得以可视化。通过对滤波器窗口宽度的选择，能够优化其在dq坐标系下的应用，确保对正弦波信号的高效滤除，消除频率的整数倍振荡。这使得FSPLL设计具有抗电网干扰的能力，即使在极端电压条件下也能实现快速且准确的正序电压检测，一个周期内即可完成。
此外，FSPLL还包括一个简单频率检测器，使得整个系统的频率适应性增强，能够在电网频率变化较大的情况下保持稳定工作。通过理论分析与实验验证，该设计显示出优异的性能，证明了它在实际应用中的鲁棒性和可靠性。
总结来说，这篇文章为电力电子系统设计提供了一种先进的正序分量检测方法，利用低通滤波技术与相锁定环路的巧妙结合，确保了在复杂电网环境下稳定、高效的信号处理能力。这对于电力系统监控、保护和控制等方面具有重要意义。
2554 IEEE TRANSACTIONS ON POWER ELECTRONICS, VOL. 25, NO. 10, OCTOBER 2010
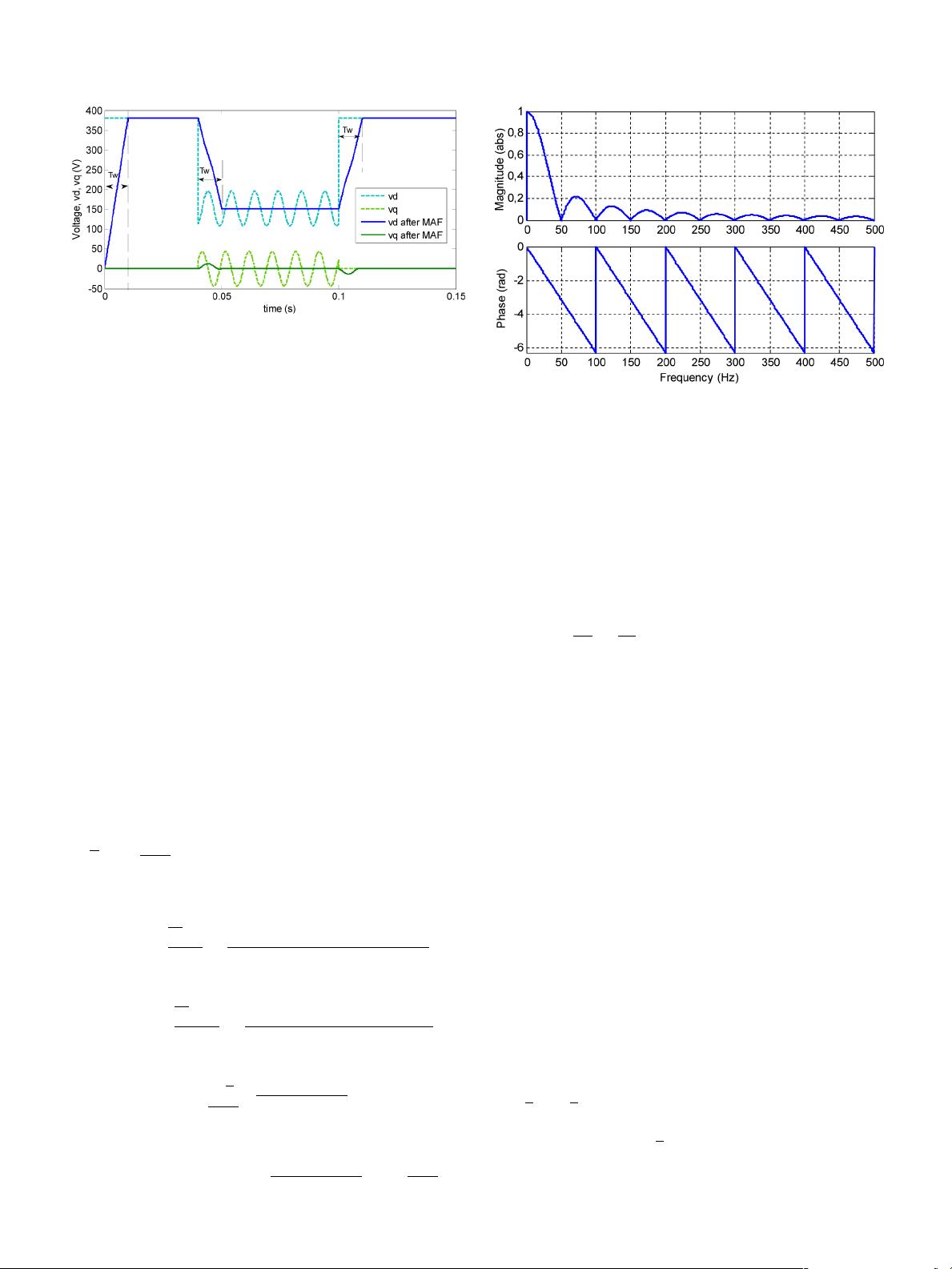
Fig. 1. Performance example of the MAF.
the larger T
w
is, the slower the detection dynamic. If the input
signal contains sinusoidal components, whose frequency is an
integer multiple of the equivalent frequency of the MAF (f
w
=
1/T
w
), the output signal will be free of oscillations containing
only the mean value of the input signal. The MAF will need
a period of time T
w
to gather the data and obtain the correct
output, hence, this is the delay produced by the MAF.
In Fig. 1, grid voltages suffer an asymmetric voltage dip
(20%, 40%, and 60%) that generates a negative sequence in the
dq components. The window width is 0.01 s, that is half the
input signal period and exactly the negative-sequence period.
The MAF can eliminate the input oscillation after gathering the
data. When the input signal changes suddenly, the output of
the MAF has an error during T
w
until the window contains an
integer number of oscillations and the MAF obtains again the
mean value.
Selection of the window width is an important issue. Depend-
ing on this, the MAF is able to perform as an ideal low-pass filter
for some input frequency components.
For a better understanding of the MAF, the transfer function
has been obtained and analyzed. Given an input signal
x(t)=A sin(ωt + θ
0
) (4)
with ω =2π/T . The output of the MAF will be
x(t)=
A
ωT
w
{cos[ω(t − T
w
)+θ
0
] − cos(ωt + θ
0
)}. (5)
Applying the Laplace transform to (4) and (5), the transfer
function for θ
0
=0becomes
G
MAF
(s)=
X(s)
X(s)
=
ω sin(ωT
w
) − s[1 −cos(ωT
w
)]
ω
2
T
w
. (6)
Substituting s = jω
G
MAF
(jω)=
X(jω)
X(jω)
=
sin(ωT
w
) − j[1 − cos(ωT
w
)]
ωT
w
. (7)
The magnitude and phase expressions are as following:
|G
MAF
(jω)| =
√
2
ωT
w
1 − cos(ωT
w
) (8)
and
ϕ[G
MAF
(jω)] = −arctan
1 − cos(ωT
w
)
sin(ωT
w
)
= −
ωT
w
2
. (9)
Fig. 2. Frequency response of the MAF.
The MAF is a finite-impulse response (FIR) filter that, as shown
in (9), has linear-phase response, being the time of the delay
constant and known.
From (8), the output magnitude of the MAF is zero whenever
[1 − cos(ωT
w
)] = 0, i.e.,
ωT
w
= k2π for k =1, 2, 3,... (10)
or
T
w
T
=
f
f
w
= k for k =1, 2, 3,.... (11)
Fig. 2 shows the frequency response of the MAF. In this rep-
resentation, the window width of the MAF is T
ω
= T , being T
the input signal period. Observe that the frequency components
that comply with (11) are canceled completely; therefore, all
of the input signal are harmonics. The frequency components
close to the filter-node frequencies will not be canceled, but
very attenuated. Additionally, according to (9), the MAF shows
linear phase.
When using the MAF to filter dq components, if T
w
= T/2,
the dq even-order oscillations from odd-order harmonics and
the negative sequence would be completely removed. If even-
order harmonics with significant amplitudes are expected, the
window width of the MAF should be increased to T
w
= T .
IV. FSPLL
Fig. 3 shows the structure of the proposed positive-sequence
detector. First, the grid voltage vector is transformed using a
synchronous reference frame rotating at fundamental frequency
(ω
f
) and with an arbitrary angular position (θ
f
). The compo-
nents v
d
and v
q
may contain oscillations due to harmonics and
a negative voltage sequence. Both components are thus filtered
through the MAF; therefore, if an appropriate window width is
used,
v
d
and v
q
will be constant and containing only the positive
sequence of the grid voltages.
As shown in Fig. 4, the
v
q
component is not necessarily zero
because the angle used in the Park transformation is arbitrary.
Thus, the voltage vector is not on the d-axis, but on another
剩余11页未读，继续阅读
2021-05-20 上传
2021-05-14 上传
2017-12-05 上传
2021-05-23 上传
2014-08-18 上传
2010-10-30 上传
点击了解资源详情
tony808
- 粉丝: 0
- 资源: 8
我的内容管理
展开
最新资源
- JHU荣誉单变量微积分课程教案介绍
- Naruto爱好者必备CLI测试应用
- Android应用显示Ignaz-Taschner-Gymnasium取消课程概览
- ASP学生信息档案管理系统毕业设计及完整源码
- Java商城源码解析：酒店管理系统快速开发指南
- 构建可解析文本框：.NET 3.5中实现文本解析与验证
- Java语言打造任天堂红白机模拟器—nes4j解析
- 基于Hadoop和Hive的网络流量分析工具介绍
- Unity实现帝国象棋：从游戏到复刻
- WordPress文档嵌入插件：无需浏览器插件即可上传和显示文档
- Android开源项目精选：优秀项目篇
- 黑色设计商务酷站模板 - 网站构建新选择
- Rollup插件去除JS文件横幅：横扫许可证头
- AngularDart中Hammock服务的使用与REST API集成
- 开源AVR编程器：高效、低成本的微控制器编程解决方案
- Anya Keller 图片组合的开发部署记录
