MATLAB实现数字信号处理：FFT、CZT与滤波器设计

该资源是关于数字信号处理的MATLAB实现教程，重点涵盖了Z变换、离散时间系统分析以及数字滤波器设计的基础知识。实验内容包括Z变换的应用、系统阶跃响应计算、单位抽样响应求解以及频率响应的获取。 在数字信号处理领域，Z变换是分析离散时间信号和系统的重要工具。Z变换将离散时间序列转换到Z域，使得我们可以用连续的方式分析离散信号，从而更好地理解和设计离散时间系统。在MATLAB中，可以方便地使用相关函数进行Z变换的计算和系统分析。 实验一介绍了如何利用Z变换分析离散时间系统。转移函数H(z)是系统的关键参数，通常表示为B(z)除以A(z)，其中B(z)和A(z)是Z域的多项式。在MATLAB中，这些多项式的系数以向量形式存储，并且一般假设A(z)的最高次项系数为1。 实验中给出了两个实例。第一个例子演示了如何计算系统的阶跃响应。`filter`函数在这里被用来根据给定的系统函数和输入信号x(n)计算输出y(n)。这个例子使用了一个全为1的输入序列（阶跃信号），并通过`filter`函数得到系统对阶跃输入的响应。 第二个例子展示了如何获得系统的单位抽样响应h(n)。这通过`impz`函数实现，它可以直接输出h(n)的值及其对应的样本点n。在这个例子中，使用了相同的系统函数来计算单位抽样响应，并通过`stem`函数进行图形化展示。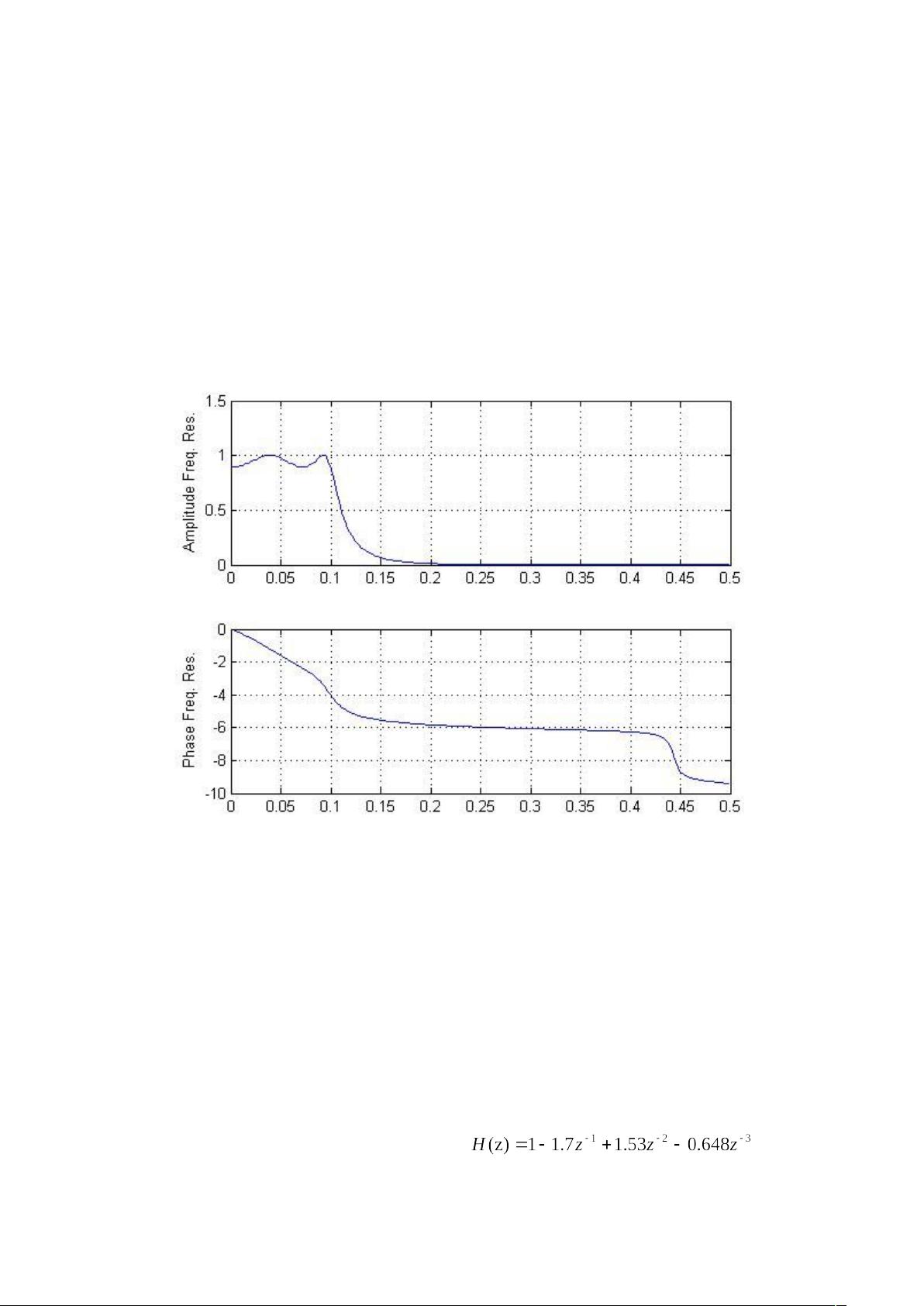 最后，获取系统频率响应是数字滤波器设计的关键步骤。`freqz`函数可以用来计算系统的频率响应H(e^(jw))，其中w是角频率。这个函数需要输入系统函数的系数以及可选参数N（采样点数）和Fs（采样频率），返回的结果是频率响应的幅度和相位。 通过这样的实验，学习者可以深入理解离散时间系统的动态特性，包括稳定性和频率选择性，这对于设计和分析数字滤波器至关重要。这些MATLAB实现不仅有助于理论学习，也方便将理论应用于实际问题，具有很好的移植性和实用性。