绿萝点云数据PCA降维与平面拟合详解

本文档主要探讨了如何利用PCA（主成分分析）算法对绿萝点云数据进行降维处理，这是一种常用的数据分析技术，尤其在图像处理、机器学习等领域有着广泛应用。PCA通过线性变换将原始高维数据映射到一组新的坐标系，其中新坐标轴的方向是由数据中最大的方差决定的，从而实现数据的降维。 首先，文档介绍了PCA的基本概念，它是通过对数据集的协方差矩阵进行特征值分解来找到最重要的特征方向。在绿萝点云数据的背景下，数据集由6维组成，包括空间坐标和法向量坐标。为了应用PCA，数据需要进行预处理，即中心化，使得每个维度的均值为零。 接下来，作者在Python环境下，使用了numpy库来进行矩阵运算，matplotlib库则用于可视化结果。程序的关键步骤包括： 1. 导入所需的库，如numpy for数值计算和matplotlib及其子库Axes3D用于3D图形展示。 2. 计算数据集X的协方差矩阵CX，这是PCA的基础，它反映了各个特征之间的线性相关性。 3. 对协方差矩阵CX进行特征值分解，得到对角矩阵D和特征向量矩阵P。特征值排序递减，反映了主成分的重要性。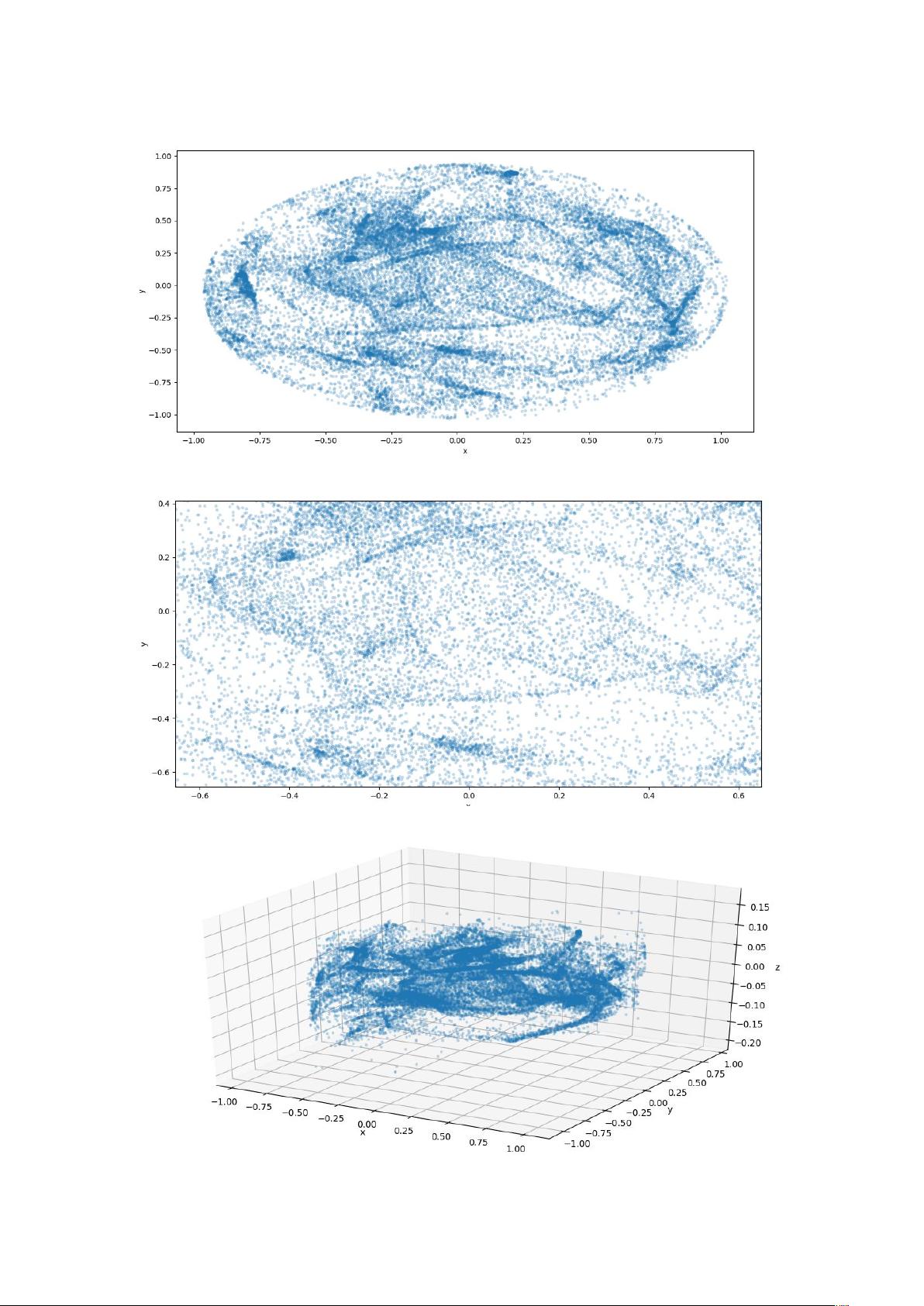 4. 选择所需数量的主成分（例如，保留第1、2主成分或第1、2、4主成分），对应地选取P矩阵中的行向量，这些行向量构成了降维后的数据映射矩阵。 5. 应用映射矩阵P对原始数据集X进行投影，得到降维后的数据集Y。 在实验的具体实现中，作者提到了使用的硬件环境（Intel Core i5-3230M CPU和AMD Radeon R5 M200/HD8500M Series显卡）以及软件环境（Python 3.6和PyCharm IDE）。通过实际编程代码展示了如何将PCA应用于绿萝点云数据的降维过程。 通过这种方法，可以显著减少数据的维度，提高处理效率，同时保留最重要的信息，这对于后续的数据分析和模型构建非常有用。此外，文档还可能包含了关于点云数据的平面拟合部分以及相关思考题，这些都是PCA降维在实际问题中的应用场景和深入理解的延伸话题。