离散时间信号处理与MATLAB应用

"该资源是关于数字信号处理的PPT课件，重点讲解了离散时间信号与系统的内容，包括离散时间信号的定义、傅立叶变换、Z变换、离散时间系统的基本概念以及系统的频率响应和系统函数。同时，PPT中还涉及到MATLAB程序的应用，用于实际的数字信号处理操作。" 在数字信号处理领域，离散时间信号是指在时间上以离散形式表示的信号，通常用于模拟信号数字化后的分析和处理。离散时间信号可以用序列x(n)来表示，其中n是离散时间样本，而T是采样周期，采样频率fs定义为1/T。离散时间信号的基础包括以下几种典型的信号类型： 1. 单位脉冲序列δ(n)，当n=0时，其值为1，其他情况下为0，它是所有离散信号的基础。 2. 单位阶跃序列u(n)，它从n=0时刻开始取值1，并保持不变，对于负数时间则为0。 3. 矩形序列RN(n)，在0到N-1之间取值1，其余为0，它代表了一个持续时间为N的矩形波形。 4. 实指数序列x(n)=a^n，其中a是常数，可以用来表示指数衰减或增长的信号。 5. 正弦序列x(n)=sin(ωn)，其中ω是数字域角频率，表示信号的振动特性。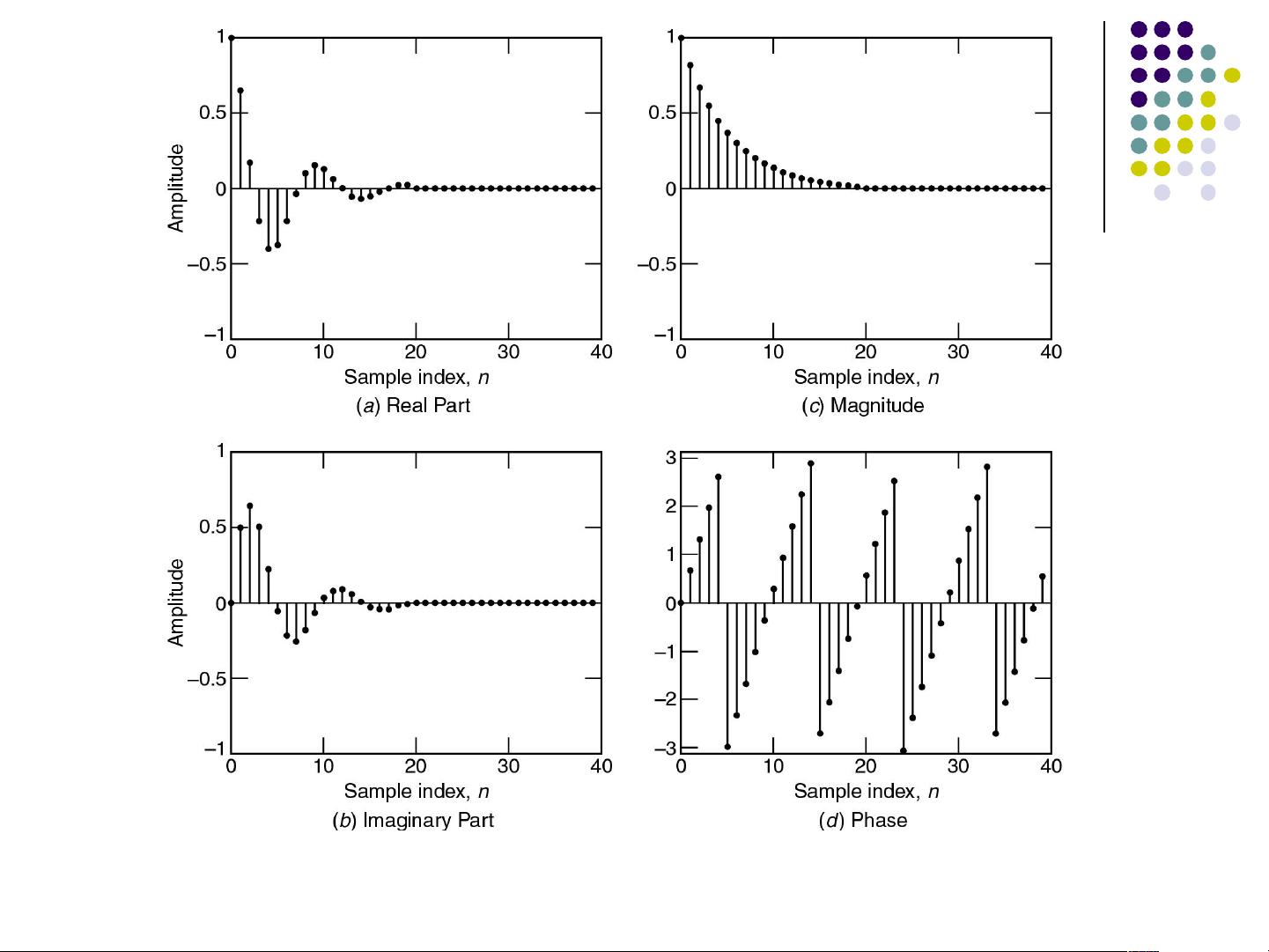 6. 复指数序列x(n)=re^(jnω0)，当r=1时，它由正弦和余弦序列构成，分别对应于信号的幅度和相位。 离散信号的傅立叶变换和Z变换是分析其频域特性的关键工具。傅立叶变换揭示了信号的频率成分，而Z变换则提供了在复平面内分析离散信号的手段，对于理解和设计数字滤波器特别有用。离散时间系统则是对输入信号进行操作的数学模型，其频率响应和系统函数H(z)定义了系统对不同频率输入的响应。 MATLAB作为强大的数值计算和信号处理工具，在数字信号处理中扮演着重要角色。通过编写MATLAB程序，可以实现对离散时间信号的运算、滤波、变换等功能，从而深入理解和应用这些理论知识。 在实际应用中，例如示例1.1中，可能利用MATLAB来计算和可视化复指数序列的幅度和相位，这有助于理解信号的频谱特性。通过这样的实践，学习者能更好地掌握离散信号处理的基本原理和方法。