应用线性代数：向量、矩阵与最小二乘课件精讲

"这是一份由Stephen Boyd和Lieven Vandenberghe教授的'应用线性代数入门'课程的幻灯片，主要关注向量、矩阵和最小二乘法。课程从基本概念开始，深入探讨了向量的定义和表示方法。 在第一部分中，向量被定义为有序数列，每个数称为元素或系数。例如，一个四维向量可以表示为： \[ \begin{bmatrix} -1.1 \\ 0.0 \\ 3.6 \\ -7.2 \end{bmatrix} \] 或者写作(-1.1, 0, 3.6, -7.2)，其中每个数字是向量的组成部分，其数量（维度或长度）决定了向量的大小。一个具有n个元素的向量被称为n-维向量，比如上面的向量就是4维向量，其第三项的值为3.6。 课程还引入符号来表示向量，如a、X、p、β等，用大写字母表示一般向量，小写字母i表示特定位置的元素，例如a3代表向量a的第三个元素，其值为3.6。向量的等号用于表示两个向量相等，即如果它们的所有分量都相等，则称这两个向量相等。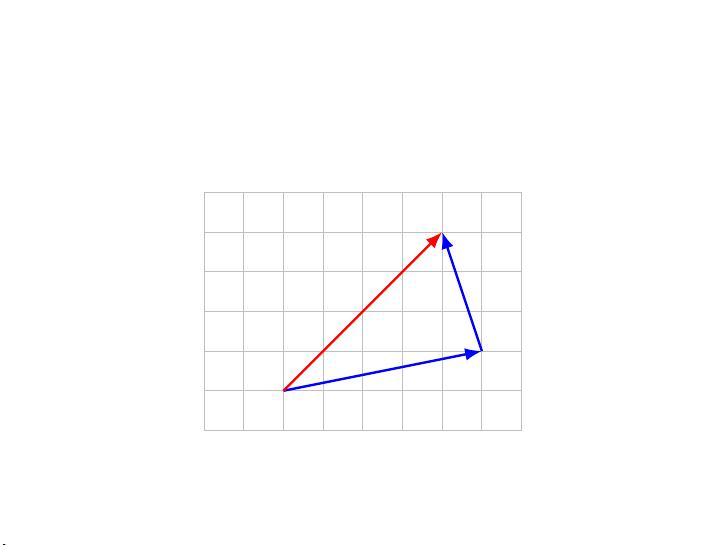 第二部分可能进一步讲解向量的运算，如加法和标量乘法，以及如何用符号表示这些运算。例如，两个相同大小的向量a和b相加可以写作a + b，而标量乘法则为a * scalar。 矩阵在课程中也占据重要地位，尽管这部分内容没有直接在提供的部分内容中提及，但通常在介绍完向量后，会涉及矩阵作为向量的集合，以及它们如何用于表示线性变换和方程组。矩阵可以用来表示多个向量的组合，其元素反映了向量之间的关系。 最后，提到的“Least Squares”可能是指最小二乘法，这是一种广泛应用于数据拟合和统计分析的优化技术，通过求解一组含有误差的数据点的最佳拟合直线或平面来解决实际问题。这部分内容将在后续的讲座中详细讨论。 总结来说，这份课件提供了一个基础框架，涵盖了线性代数中的关键概念，旨在帮助学生理解如何运用向量和矩阵解决实际问题，如工程、机器学习和数据分析中的模型构建。对于那些希望进一步探索线性代数在现代技术领域应用的人来说，这是一个宝贵的资源。"