有序链表转二叉搜索树：分治算法实现

"有序链表转换为二叉搜索树是一个常见的算法问题，涉及到数据结构和算法设计。目标是将一个已排序的链表转化为高度平衡的二叉搜索树，保证每个节点的左右子树高度差的绝对值不超过1。高度平衡的二叉搜索树能够保证查询效率较高。 在解决这个问题时，一种常用的方法是分治策略。首先，我们需要找到链表的中位数作为根节点，因为这样可以使得左右子树的节点数量接近，从而达到平衡。对于中位数的定义，如果链表长度为奇数，中位数是唯一的中间元素；如果长度为偶数，则可以选择任意一个中间元素。这是因为无论选择哪个中间元素，左子树和右子树的元素数量之差不超过1，满足平衡条件。 寻找中位数节点的过程可以使用快慢指针法。初始化两个指针，快指针`fast`每次移动两步，慢指针`slow`每次移动一步。当`fast`到达链表末尾或者其下一个节点是末尾时，`slow`指向的节点就是中位数。这个过程中，我们设定了`left`作为链表的左端点，`right`是右端点，两者之间是左闭右开的关系，这有助于我们在处理链表时更方便地定义左右子树的范围。 接下来，我们以中位数节点为根创建二叉搜索树。中位数左边的元素构成左子树，右边的元素构成右子树。然后对左右子树递归执行相同的操作，即找到新的中位数并构建子树，直到链表为空。最终，这个过程会构建出一棵高度平衡的二叉搜索树。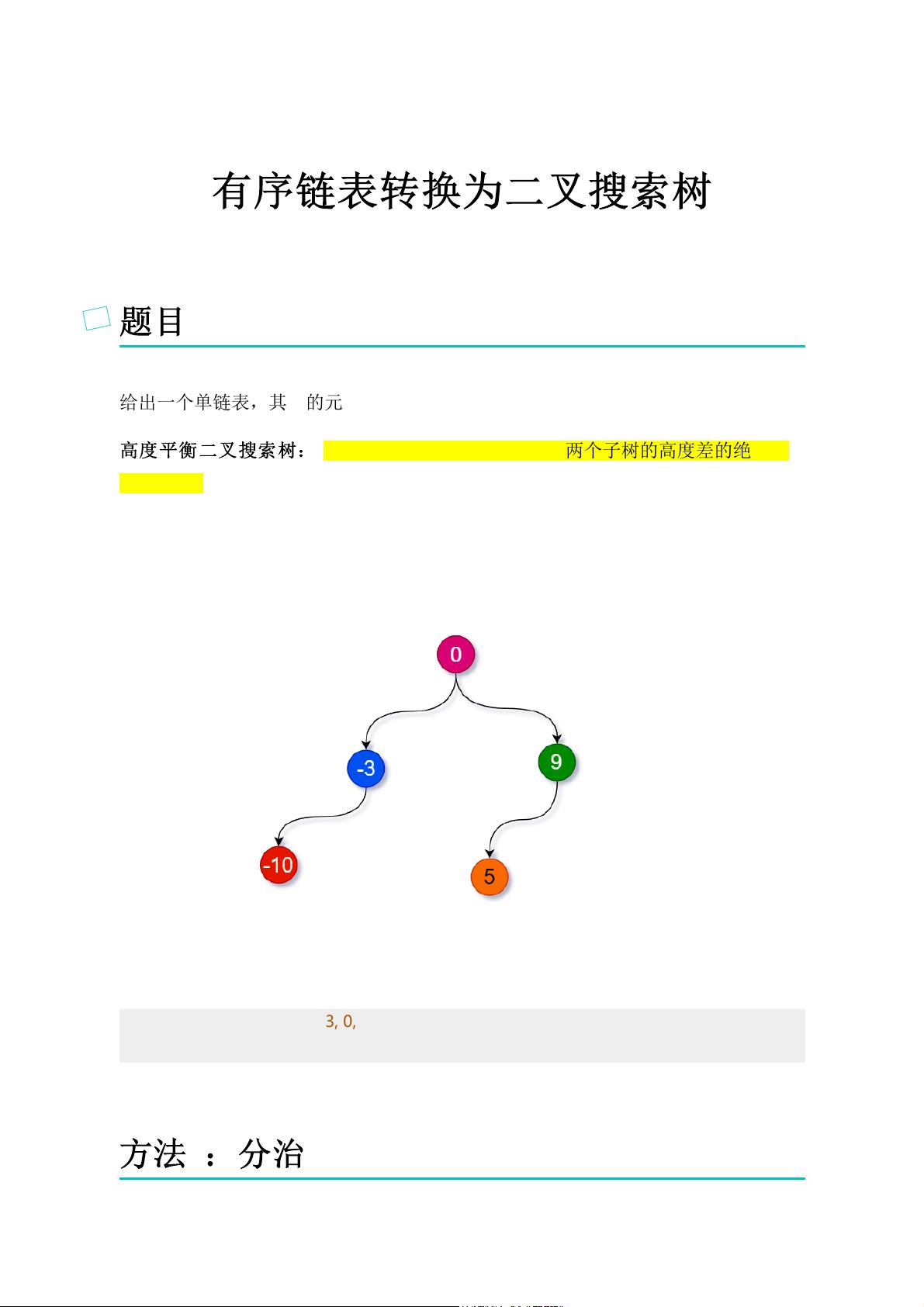 例如，在给定的示例中，有序链表`[-10,-3,0,5,9]`可以通过这种方法转化为如下的高度平衡二叉搜索树：`[0,-3,9,-10,null,5]`。在这个树中，0是根节点，-3和5分别是左子树和右子树的根，它们各自包含了小于0和大于0的元素。 总结起来，将有序链表转换为高度平衡的二叉搜索树的关键在于找到合适的中位数作为根节点，并利用分治策略递归地构建左右子树。这个过程需要对链表操作和二叉树结构有深入的理解，同时熟练掌握快慢指针等技巧，以实现高效且正确的问题解决方案。"