模糊PID控制器设计与参数自整定

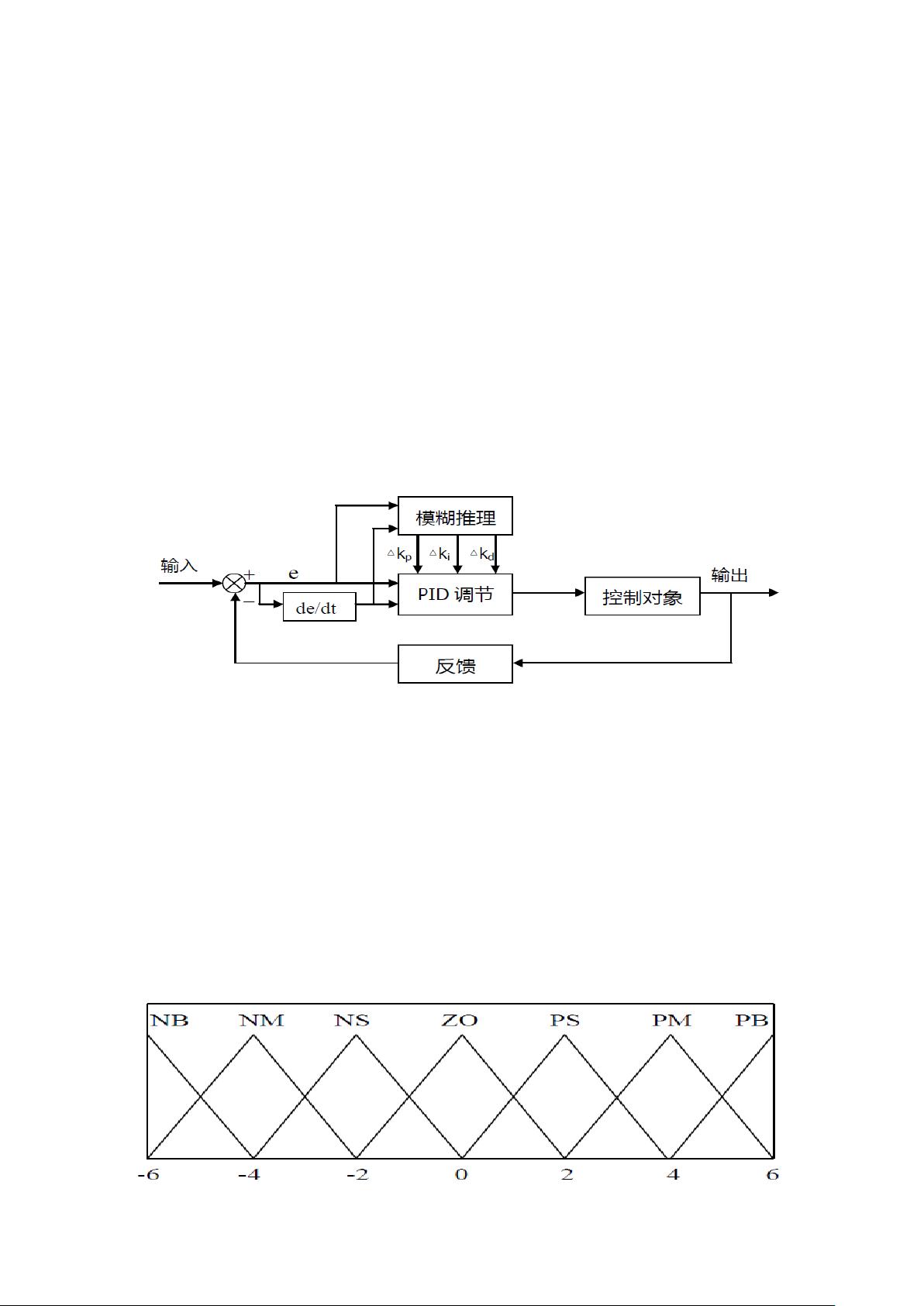
"本文主要探讨了参数自整定模糊PID控制器的设计，包括传统PID控制原理和模糊PID控制原理。文章通过MATLAB仿真展示了模糊规则在控制器中的应用，并提供了相关的仿真结果。" 1、传统PID控制原理 传统的比例积分微分（PID）控制器是一种广泛应用的反馈控制算法。其离散形式的表达式为 \( u(k) = k_p e(k) + \frac{k_i}{z} \sum_{j=0}^{k} e(j) + k_d \frac{d}{dz} ec(k) \)，其中 \( u(k) \) 是控制器在第 \( k \) 次采样的输出，\( e(k) \) 和 \( ec(k) \) 分别是系统偏差和偏差变化量，\( k_p \)、\( k_i \) 和 \( k_d \) 是比例、积分和微分系数。这些参数需要根据具体系统进行精细调整，以达到期望的控制性能。 2、模糊PID控制原理 参数自整定模糊PID控制器引入了模糊逻辑，其基本思路是建立PID参数（\( kp \)、\( ki \)、\( kd \)）与误差 \( e \) 和误差变化率 \( ec \) 的模糊关系。控制器在运行过程中实时监测这两个变量，然后基于模糊控制规则动态调整参数，使得 \( kp \)、\( ki \) 和 \( kd \) 能够适应系统状态的变化。公式表示为 \( kp = kp_0 + \Delta kp \)，\( ki = ki_0 + \Delta ki \)，\( kd = kd_0 + \Delta kd \)，其中 \( kp_0 \)、\( ki_0 \)、\( kd_0 \) 是初始参数值。 2.1 输入输出变量的模糊隶属度函数 为了实现模糊控制，需要定义输入变量（误差 \( e \) 和误差变化率 \( ec \)）和输出变量（参数修正量 \( \Delta kp \)、\( \Delta ki \)、\( \Delta kd \)）的模糊子集。这里采用的语言变量有7个，分别是{正大(PB)、正中(PM)、正小(PS)、零(ZE)、负小(NS)、负中(NM)、负大(NB)}，对应的模糊论域是均匀且全交叠的三角形隶属度函数。 2.2 模糊控制规则 模糊控制规则是根据偏差和偏差变化率对PID参数的具体要求以及实际经验得出的。例如，表1、表2和表3列出了修正量 \( \Delta kp \)、\( \Delta ki \) 和 \( \Delta kd \) 的模糊控制规则，这些规则描述了在不同偏差和偏差变化率情况下，参数如何调整以优化控制效果。 模糊PID控制器通过模糊逻辑实现了参数的自整定，可以根据系统的实时状态动态调整PID参数，以提高控制性能和适应性。MATLAB仿真是验证和优化这种控制策略的有效工具，可以提供关于控制器性能的直观理解。