the underlying Sparkle permutation (and thus the rate and capacity is different) and the size of
the authentication tag. As a naming convention, we used Schwaemmr-c, where 𝑟 refers to the
size of the rate and 𝑐 to the size of the capacity in bits. Similar as for hashing, we use the big
version of Sparkle for initialization, separation between processing of associated data and secret
message, and finalization, and the slim version of Sparkle for updating the intermediate state
otherwise. Table 2.3 gives an overview of the parameters of the Schwaemm instances. The data
limits correspond to 2
64
blocks of 𝑟 bits rounded up to the closest power of two, except for the
high security Schwaemm256-256 for which it is 𝑟 × 2
128
bits.
Table 2.3: The instances we provide for authenticated encryption together with their (joint) security
level in bit with regard to confidentiality and integrity and the limitation in the data (in bytes) to
be processed. The first line refers to our primary member, i.e. Schwaemm256-128.
𝑛 𝑟 𝑐 |𝐾| |𝑁| |𝑇 | security data limit (in bytes)
Schwaemm256-128 384 256 128 128 256 128 120 2
68
Schwaemm192-192 384 192 192 192 192 192 184 2
68
Schwaemm128-128 256 128 128 128 128 128 120 2
68
Schwaemm256-256 512 256 256 256 256 256 248 2
133
2.3.2 The Algorithms
The main difference between the Beetle mode and duplexed sponge modes is the usage of a
combined feedback 𝜌 to differentiate the ciphertext blocks and the outer part of the states. This
combined feedback is created by applying the function FeistelSwap to the outer part of the state,
which is computed as
FeistelSwap(𝑆) = 𝑆
2
‖(𝑆
2
⊕ 𝑆
1
) ,
where 𝑆 ∈ F
𝑟
2
and 𝑆
1
‖𝑆
2
= 𝑆 with |𝑆
1
| = |𝑆
2
| =
𝑟
2
. The feedback function 𝜌: (F
𝑟
2
×F
𝑟
2
) → (F
𝑟
2
×F
𝑟
2
)
is defined as 𝜌(𝑆, 𝐷) = (𝜌
1
(𝑆, 𝐷), 𝜌
2
(𝑆, 𝐷)), where
𝜌
1
: (𝑆, 𝐷) ↦→ FeistelSwap(𝑆) ⊕ 𝐷, 𝜌
2
: (𝑆, 𝐷) ↦→ 𝑆 ⊕ 𝐷 .
For decryption, we have to use the inverse feedback function 𝜌
′
: (F
𝑟
2
× F
𝑟
2
) → (F
𝑟
2
× F
𝑟
2
) defined
as 𝜌
′
(𝑆, 𝐷) = (𝜌
′
1
(𝑆, 𝐷), 𝜌
′
2
(𝑆, 𝐷)), where
𝜌
′
1
: (𝑆, 𝐷) ↦→ FeistelSwap(𝑆) ⊕ 𝑆 ⊕ 𝐷, 𝜌
′
2
: (𝑆, 𝐷) ↦→ 𝑆 ⊕ 𝐷 .
After each application of 𝜌 and the additions of the domain separation constants, i.e., before
each call to the Sparkle permutation except the one for initialization, we prepend a rate whitening
layer which XORs the value of 𝒲
𝑐,𝑟
(𝑆
𝑅
) to the outer part, where 𝑆
𝑅
denotes the internal state
corresponding to the inner part. For the Schwaemm instances with 𝑟 = 𝑐, we define 𝒲
𝑐,𝑟
: F
𝑐
2
→ F
𝑟
2
as the identity (i.e., we just XOR the inner part to the outer part). For Schwaemm256-128, we
define 𝒲
128,256
(𝑥, 𝑦) = (𝑥, 𝑦, 𝑥, 𝑦), where 𝑥, 𝑦 ∈ F
64
2
. Note that this tweak can still be described
in the Beetle framework as the prepended rate whitening can be considered to be part of the
definition of the underlying permutation.
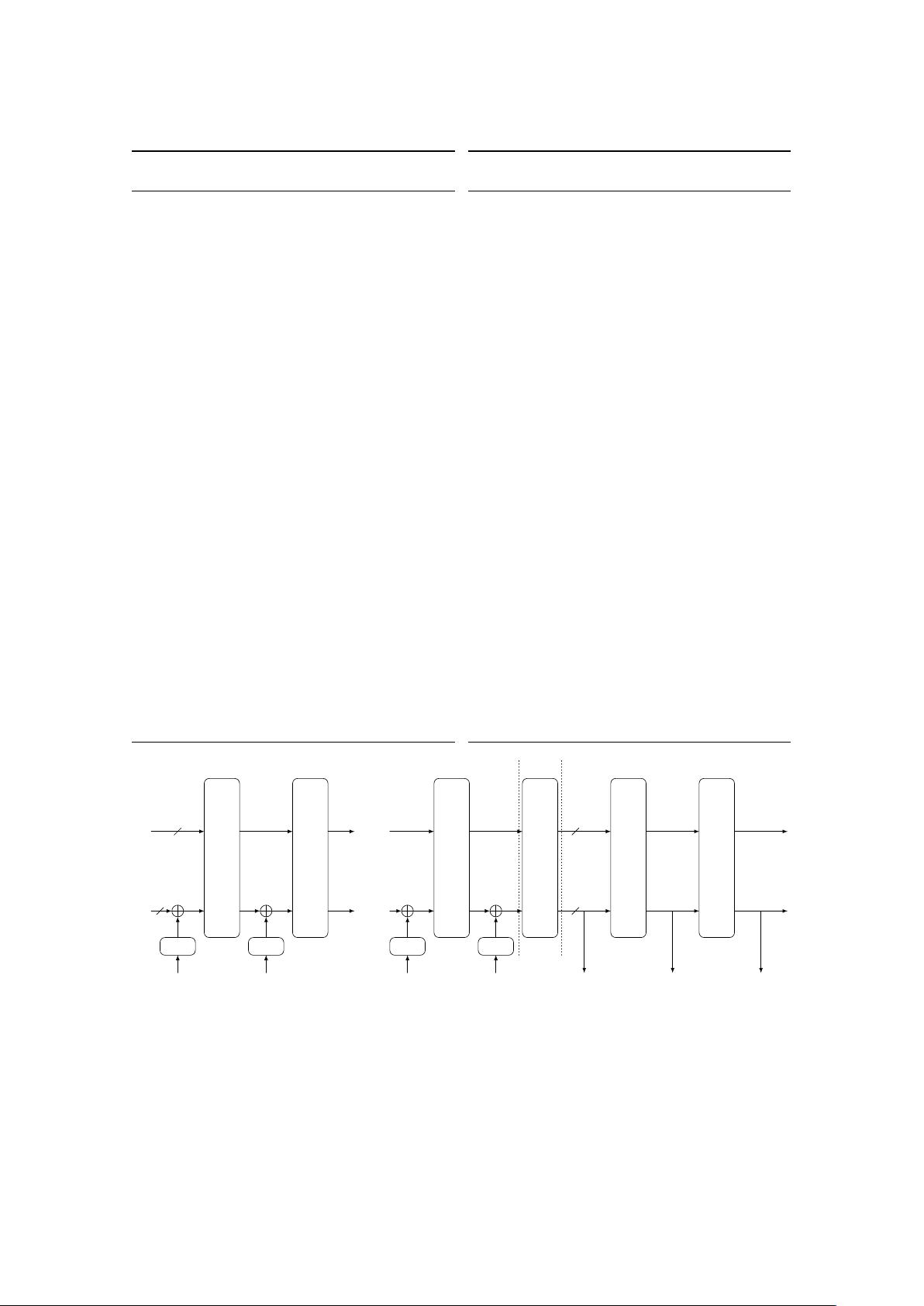
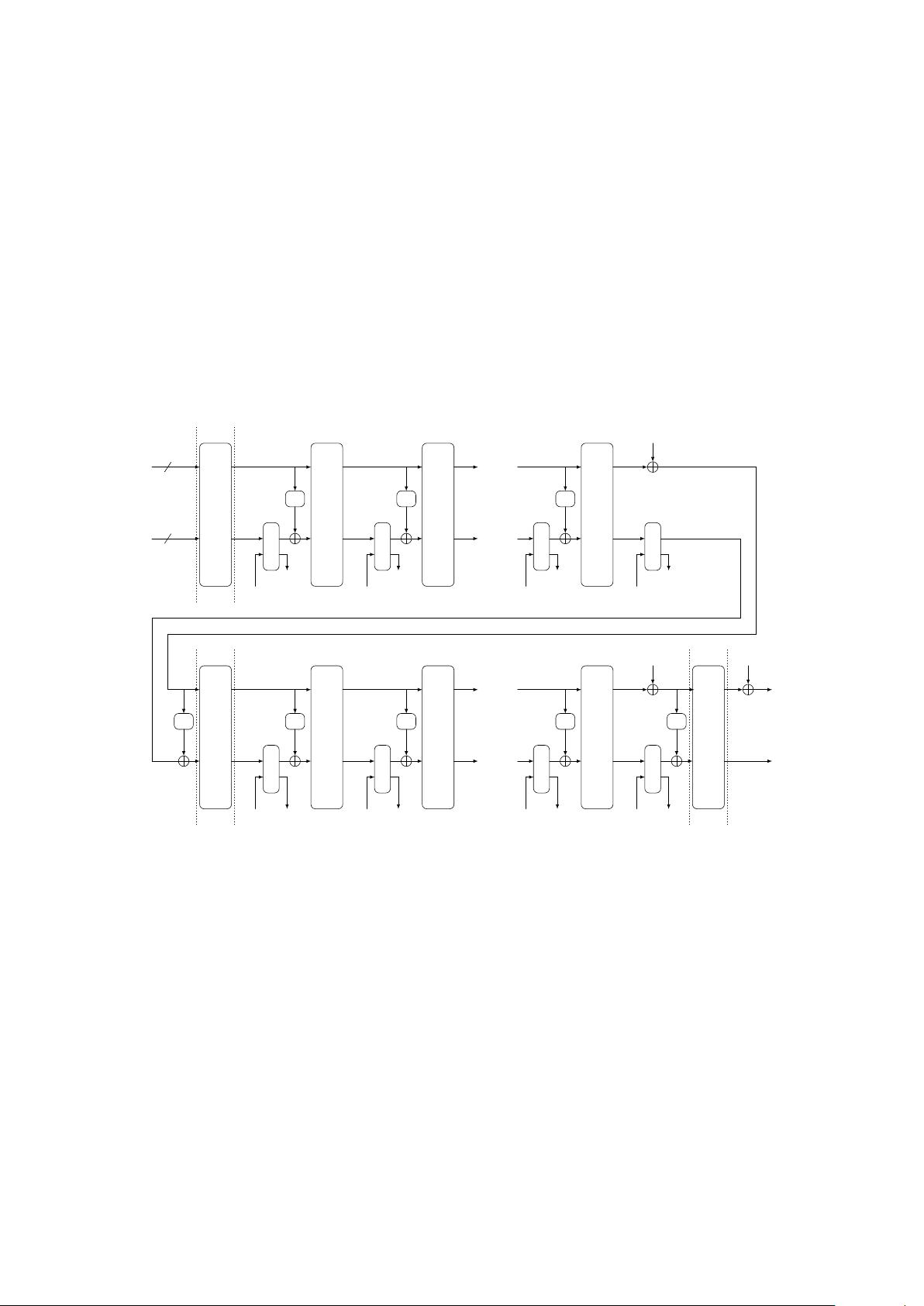
Figure 2.5 depicts the mode for our primary member Schwaemm256-128. The formal spec-
ifications of the encryption and decryption procedures of the four family members are given in
Algorithms 2.13-2.20.
14