时间序列分析：平稳性检验与ARMA模型构建

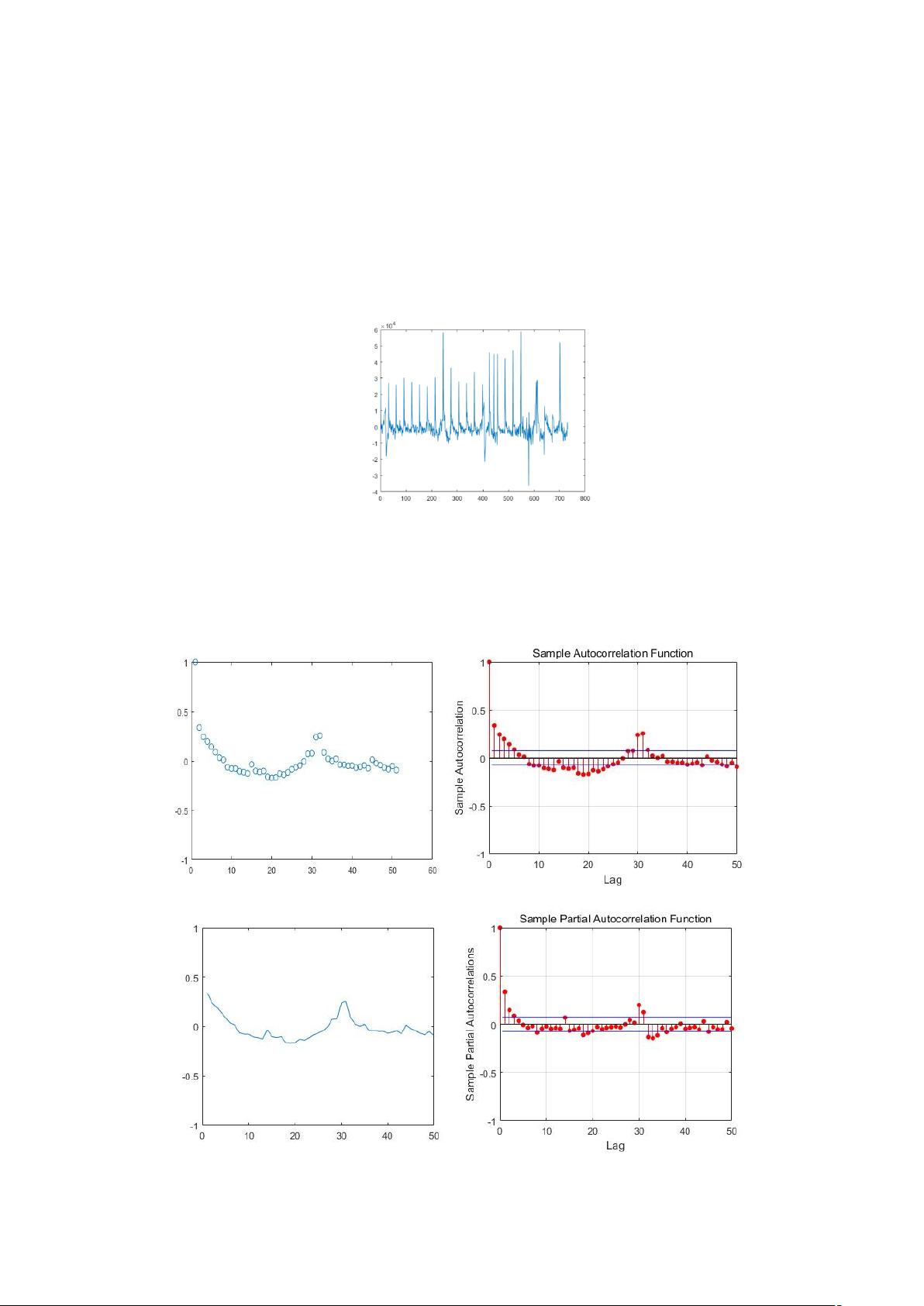
本篇文档主要涉及时间序列分析中的一个重要课题——模型的建立和定阶，特别是在使用Matlab软件进行处理。作者以李逢君（2016060601010）的身份分享了一种方法，即通过最小二乘法拟合多项式来去除时间序列的趋势项，同时利用滑动平均消除周期性。在作业中，数据被处理得较为平滑，以便进行后续分析。 在数据预处理阶段，作者展示了去除趋势和周期性后的时间序列数据以及其自相关系数图（图1），这有助于了解数据的动态特性。数字特征的估计部分，作者应用了书中算法对自相关函数（图2）和偏相关函数（图3）进行了计算，并将结果与Matlab内置函数的结果进行了对比，以验证方法的有效性。 对于平稳性检验，自相关函数和偏相关函数表现出“拖尾性”，这表明可能存在自回归移动平均（ARMA）模型的潜在结构。作者采用了逆序检验法，通过选取样本的前720项并分为20组，计算出的统计量Z值为-0.2920。根据显著性水平α=0.05，由于|Z|=0.2920小于临界值1.96，表明序列无明显趋势，从而判断该序列是平稳的。 代码实现部分展示了主函数和逆序检验函数的具体实现。主函数`load('data.mat')`用于加载数据，`nixujianyan`函数负责执行逆序检验，它将数据分割成多个子序列，计算每个子序列的均值和方差，然后通过比较这些统计量来判断序列的平稳性。该过程使用了布尔矩阵`a`和`b`来记录子序列间的相对关系，以及`A`、`B`、`u`和`r`等变量存储检验结果。 本篇文档详细介绍了如何使用最小二乘法、滑动平均等技术处理时间序列数据，通过数字特征估计和平稳性检验确定模型的形式，以及在Matlab中实际操作的代码实现。这对于理解和应用时间序列分析，特别是使用ARMA模型建模具有重要的参考价值。