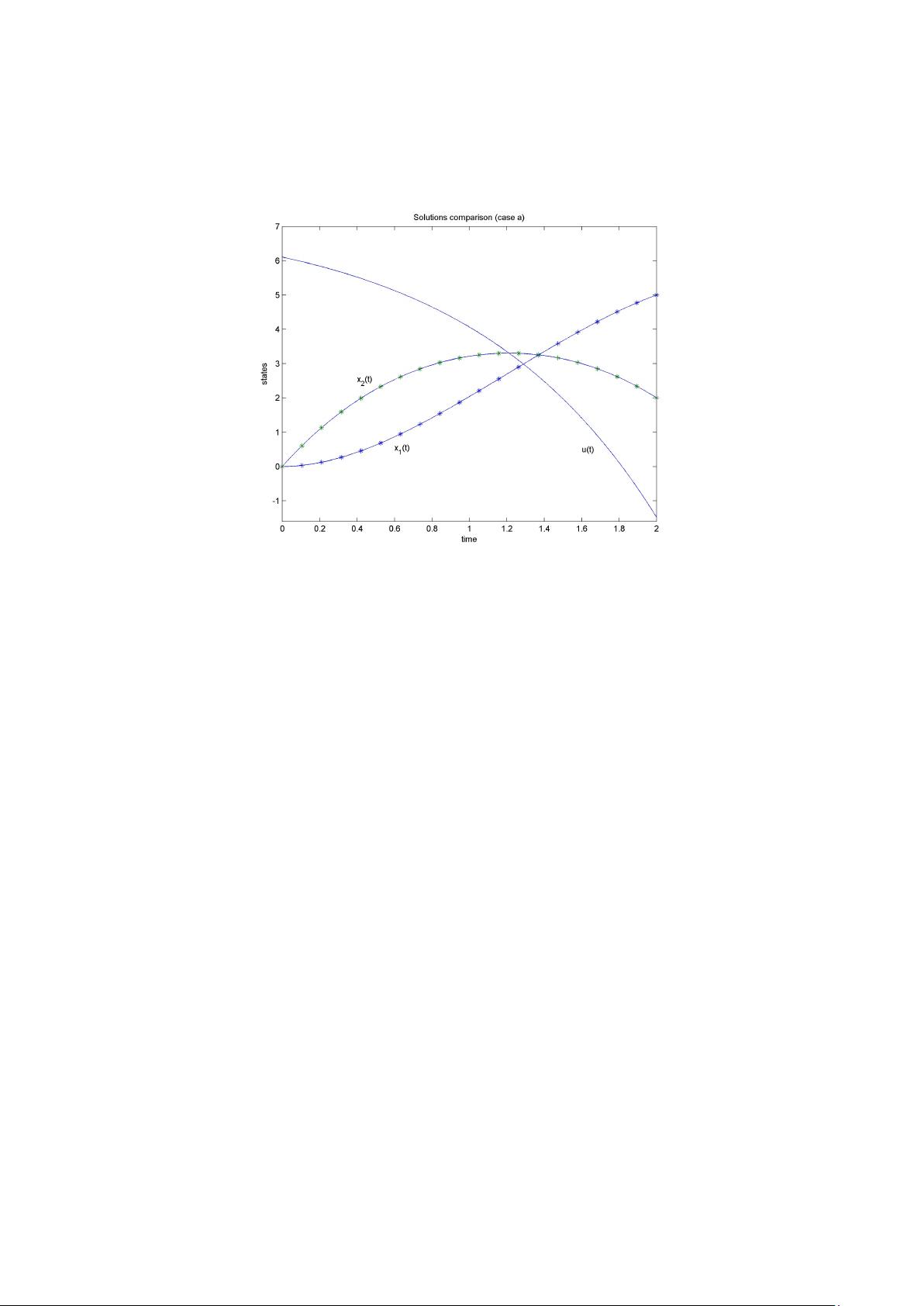
MATLAB在最优控制问题中的数值解法

"该资源是一本关于使用 MATLAB 解决最优控制问题的PDF文档，主要介绍如何利用 MATLAB 的间接方法来解决这一领域的复杂问题。书中涵盖了最优控制理论的基础，以及随着计算机技术的发展，它在生物系统、通信网络和社会经济系统等多学科应用中的广泛使用。作者强调，越来越多的人需要学习如何数值求解最优控制问题。" 正文: 最优控制理论自四十年前发展以来，已经成为一个成熟的研究领域。随着计算机技术的进步，最优控制在多个学科的应用中扮演了重要角色，例如在生物系统工程、通信网络设计和社会经济政策制定等方面。因此，理解和掌握如何数值求解最优控制问题变得越来越重要。 早期的经典著作如[1]，首次系统地介绍了最优控制的理论和许多有趣的实例，包括时间最优、燃料最优以及线性二次调节器（LQR）问题。这些书籍不仅提供了必要的条件，还尽可能给出了明确的解决方案。后来的[2]是一本简洁而优秀的工程实践导向的书籍，它引入了几种迭代算法，使得数值求解问题变得更加可行。 最近的文献[3]则进一步利用 MATLAB 这一强大的数值计算工具来解决最优控制问题。MATLAB 的使用简化了问题求解的过程，使得非专业背景的用户也能更方便地进行计算。在 MATLAB 中，可以利用内置的优化工具箱，如 fmincon、fminunc 等函数，结合动态系统的状态空间模型，来实现对最优控制问题的求解。 对于间接方法，通常涉及到拉格朗日乘子法和庞加莱-贝尔曼方程（Pontryagin's Maximum Principle）。这些方法通过构建哈密顿函数并寻找其最大值来寻找最优控制策略。在 MATLAB 中，可以通过设置适当的约束条件，运用动态规划或直接线性二次型二次规划（LQG）方法来求解这类问题。 此外，书中可能还会涵盖动态规划（Dynamic Programming）的概念，这是解决最优控制问题的一种重要方法，特别是对于离散时间和连续时间的系统。这种方法通过将整个问题分解为一系列子问题，逐个解决以找到全局最优解。 为了实际应用这些方法，读者需要了解如何建立系统的状态方程和性能指标，并能够将这些数学表达式转化为 MATLAB 可以处理的形式。这通常涉及到微分方程的解析或数值积分，以及矩阵运算的知识。 使用 MATLAB 解决最优控制问题的书籍如所描述的那样，旨在提供一个实用的平台，帮助读者理解和应用数值方法解决复杂的控制问题。通过学习，读者不仅可以掌握最优控制的基本理论，还能获得实际编程和调试经验，从而在实际工程或科研项目中有效地应用这些工具。