因果推理及其在公平性和防御对抗样本方面的应用简介

因果推理是一种用于确定因果关系的方法和工具集。它包括结构方程模型（SEM）、混杂和干预分析、工具变量和反事实分析等。在公平性和防御对抗样本方面，我们可以利用因果推理来评估和预测各种社会政策和决策对于不同人群的影响，以及检验和纠正因社会偏见而引起的数据问题。这篇摘自知乎、《统计因果推理》和因果推理课程等的部分内容，总结了因果推理的概念和在公平性和防御对抗样本方面的应用。 一、因果推理简介 因果推理是一种用于判断在特定条件下，某个因素对另一个因素产生的影响程度的方法。它的应用领域非常广泛，涵盖了社会学、经济学、医学、心理学等领域。因果推理的核心问题是确定变量X对变量Y的因果影响。常见的因果推理方法包括结构方程模型、混杂和干预分析、工具变量和反事实分析等。 二、因果推理与公平性 在公平性领域，因果推理可以用来评估和预测各种社会政策和决策对于不同人群的影响。例如，在教育公平领域，我们可以利用因果推理方法来评估不同学校政策对于不同学生群体的影响，以及检验和纠正因社会偏见而引起的数据问题。此外，在法律领域，因果推理方法也可以用来评估司法决策对不同族裔、性别和年龄群体的影响，以及检验和纠正因社会偏见而引起的司法不公问题。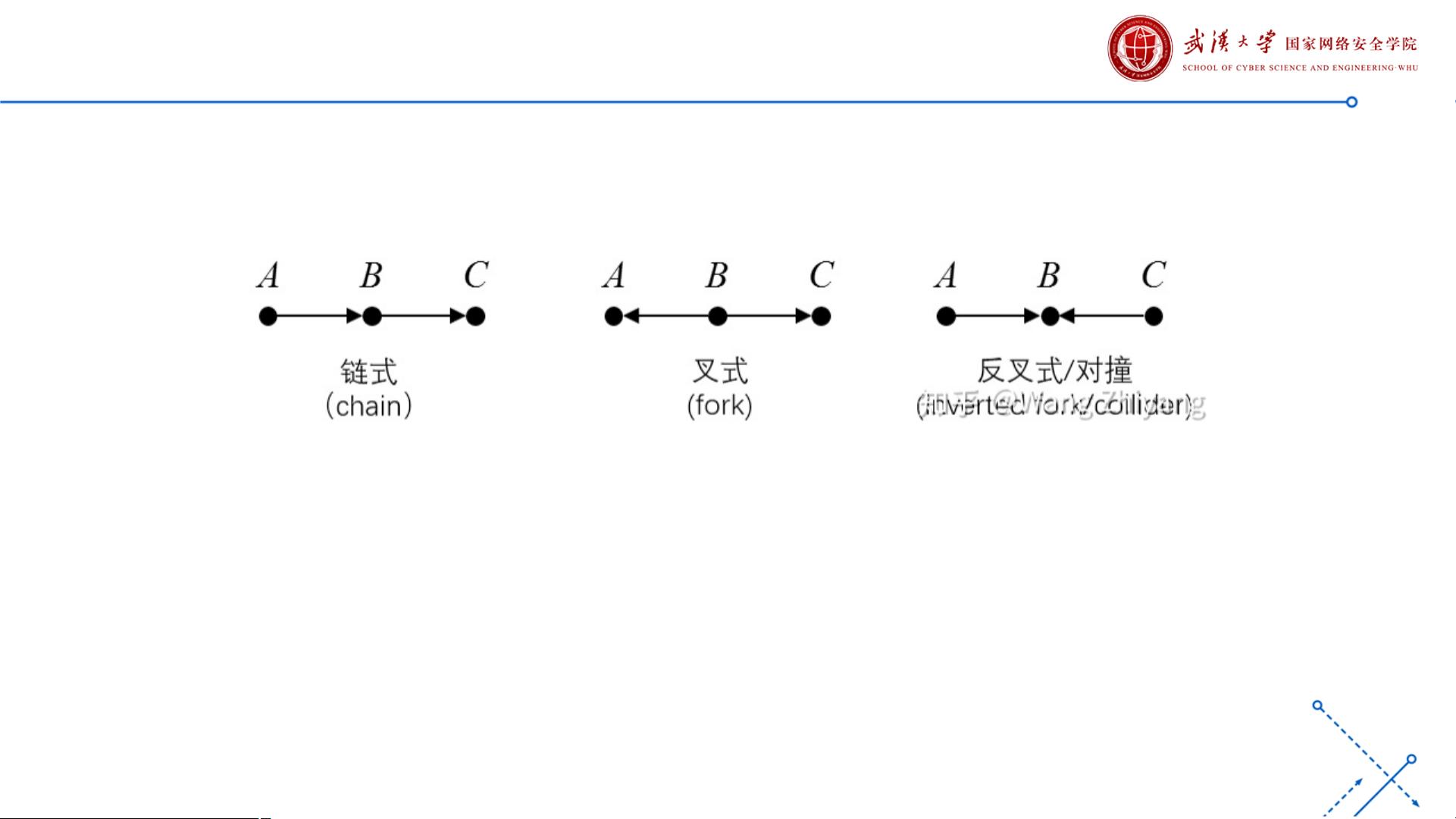 因果推理的概念 结构因果模型 结构因果模型是一种用来描述和分析不同变量之间因果关系的数学模型。它将变量之间的关系表示为一个有向图，通过观察变量之间的条件独立性来推断它们之间的因果关系。结构因果模型的核心问题是如何从观察到的数据中推断出因果关系。常见的结构因果模型包括链式结构、叉式结构和对撞结构。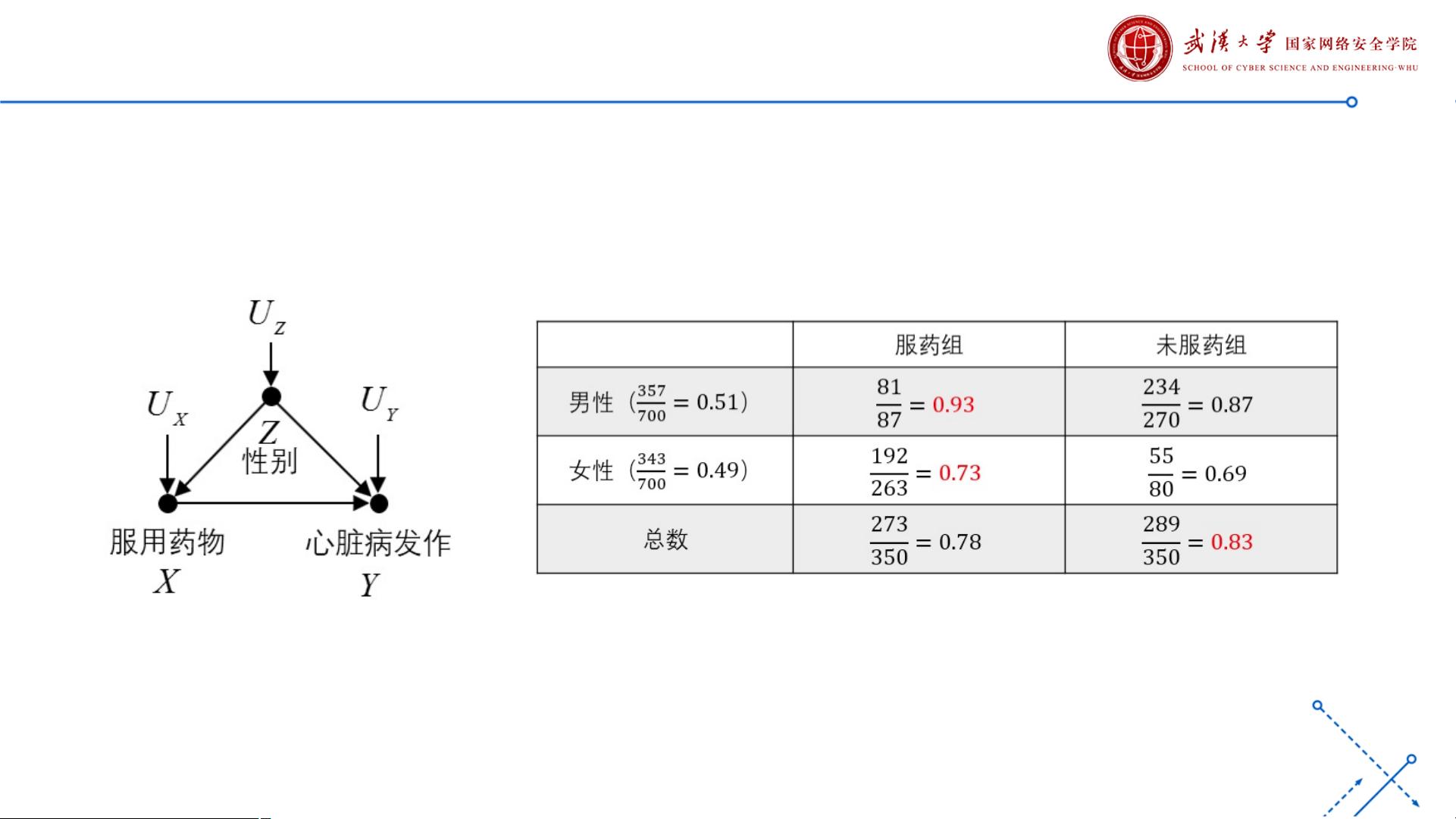 混杂与干预 混杂是指变量之间存在交叉影响，使得我们无法准确判断它们之间的因果关系。干预是指主动改变某个变量，以便判断它对其他变量的因果影响。混杂和干预是因果推理的重要工具，可以帮助我们更准确地判断变量之间的因果关系。 因果推理的其他应用 除了在公平性领域，因果推理还可以应用于许多其他领域。在医学领域，因果推理可以用来评估不同治疗方案对患者生存率的影响。在环境科学领域，因果推理可以用来评估不同环境政策对大气污染和气候变化的影响。在金融领域，因果推理可以用来评估不同投资策略对股票收益率的影响。因果推理的应用领域非常广泛，可以帮助我们更准确地理解和预测各种复杂系统的行为。 三、反事实 反事实是指从观察到的数据中推断未观察到的数据的方法。因果推理的核心问题是如何从观察到的数据中推断出因果关系。反事实是因果推理的重要方法之一，可以帮助我们更准确地判断变量之间的因果关系。通过对不同干预方案的计算和比较，我们可以判断不同干预方案对变量之间的因果影响。 结构因果模型 结构因果模型是一种用来描述和分析不同变量之间因果关系的数学模型。它将变量之间的关系表示为一个有向图，通过观察变量之间的条件独立性来推断它们之间的因果关系。常见的结构因果模型包括链式结构、叉式结构和对撞结构。链式结构是指信息从变量A经过“中介”B流向C，因此A和C是相关的。条件独立性的观察是指如果变量A和C之间只有一条单向路径，B是截断这条路径的任意一组变量，则以B=b为条件时，A和C是独立的。 四、结论 因果推理是一种用于判断因果关系的方法和工具集，包括结构方程模型、混杂和干预分析、工具变量和反事实分析等。在公平性和防御对抗样本方面，我们可以利用因果推理来评估和预测各种社会政策和决策对于不同人群的影响，以及检验和纠正因社会偏见而引起的数据问题。因果推理的概念和应用领域非常广泛，可以帮助我们更好地理解和预测各种复杂系统的行为。因此，因果推理是一种非常重要的统计分析方法，值得我们深入学习和应用。