二叉树遍历详解：先序、中序、后序与层次遍历

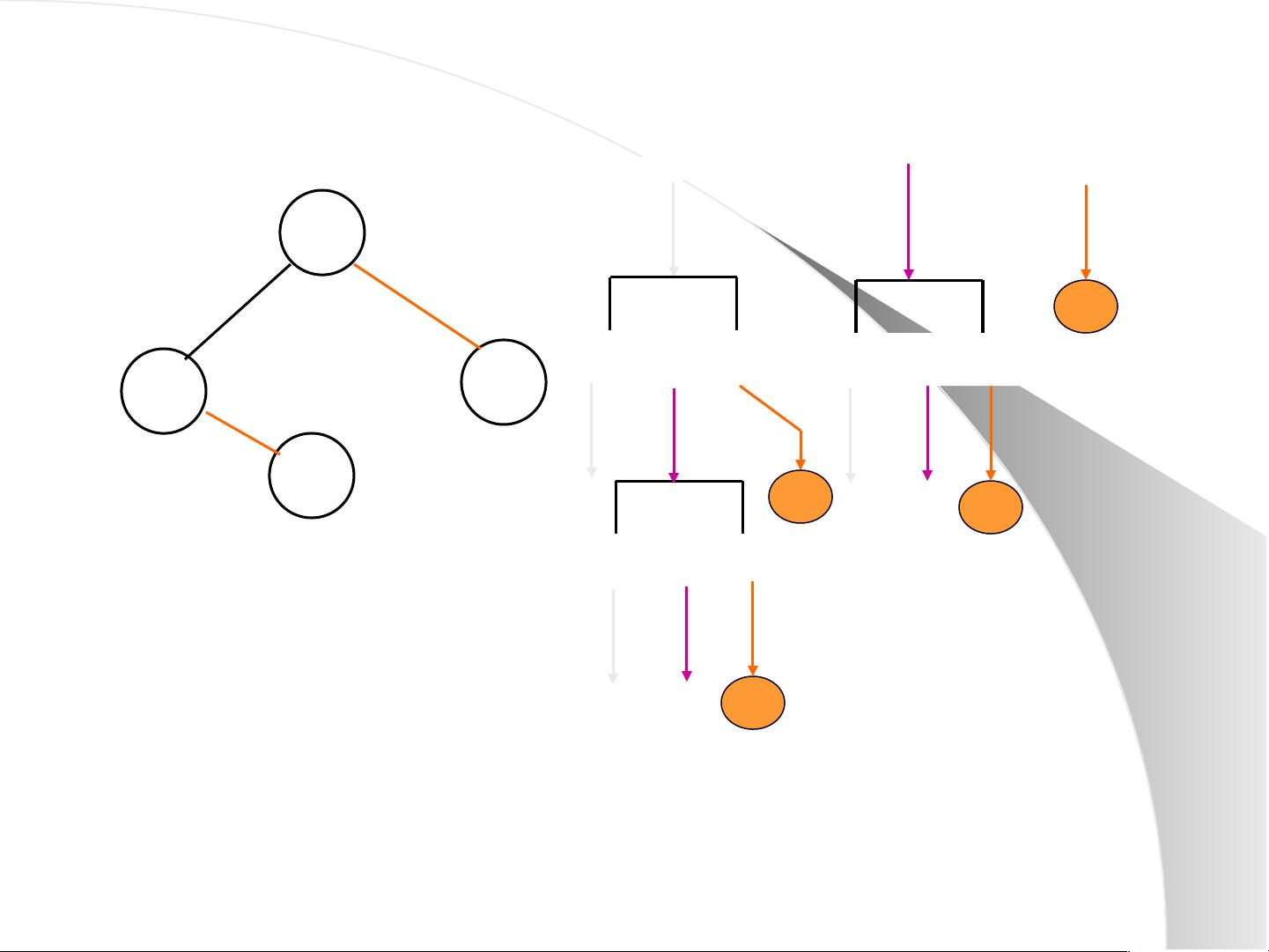
"数据结构课件，包含大学课程中的关于树和二叉树的遍历方法，包括先序遍历、中序遍历、后序遍历和按层次遍历的详细解释及示例。标签涉及C和vc语言。" 在计算机科学中，数据结构是组织和管理大量数据的有效方式，而树和二叉树是数据结构中非常重要的概念。树是一种非线性的数据结构，由结点（或称节点）和边组成，每个结点可以有零个或多个子结点。二叉树是特殊类型的树，每个结点最多只有两个子结点，通常称为左子结点和右子结点。 1. **先序遍历（Preorder Traversal）** 先序遍历的顺序是：访问根结点 -> 先序遍历左子树 -> 先序遍历右子树。在递归实现中，通常采用以下步骤： - 如果结点不为空，访问该结点 - 对左子树进行先序遍历 - 对右子树进行先序遍历 在代码实现中，如C语言，可以定义一个函数`void preorder(JD* bt)`，其中`JD`是结点类型，`bt`是树的根结点。递归地调用该函数，直到所有结点都被访问。 2. **中序遍历（Inorder Traversal）** 中序遍历的顺序是：中序遍历左子树 -> 访问根结点 -> 中序遍历右子树。对于二叉搜索树（Binary Search Tree, BST），中序遍历会得到结点从小到大的顺序。非递归实现通常需要用到栈来辅助操作，步骤如下： - 将根结点入栈 - 当栈不空时，执行以下操作： - 弹出栈顶元素，如果为空指针，说明已经遍历完该子树，跳出循环 - 否则，访问该结点，然后将它的右子结点入栈，再将左子结点入栈 3. **后序遍历（Postorder Traversal）** 后序遍历的顺序是：后序遍历左子树 -> 后序遍历右子树 -> 访问根结点。在二叉树中，后序遍历通常用于计算表达式树的结果。递归实现类似先序遍历，但访问根结点的动作放在最后。 4. **按层次遍历（Level Order Traversal）** 按层次遍历是从树的顶层开始，自上而下，从左到右访问每一个结点。这可以通过队列来实现，将根结点放入队列，然后每次取出队首元素，将其子结点加入队列，直到队列为空。 遍历二叉树的方法在许多实际应用中都非常关键，例如在搜索、排序和构建数据索引等操作中。理解并能灵活运用这些遍历算法对于解决实际问题非常重要。在C或vc++等编程环境中，可以利用递归或栈/队列等数据结构来实现这些遍历方法。在给定的课件中，提供了各种遍历方式的示例，有助于深入理解和掌握这些概念。