Delaunay三角剖分详解：概念、准则与特性

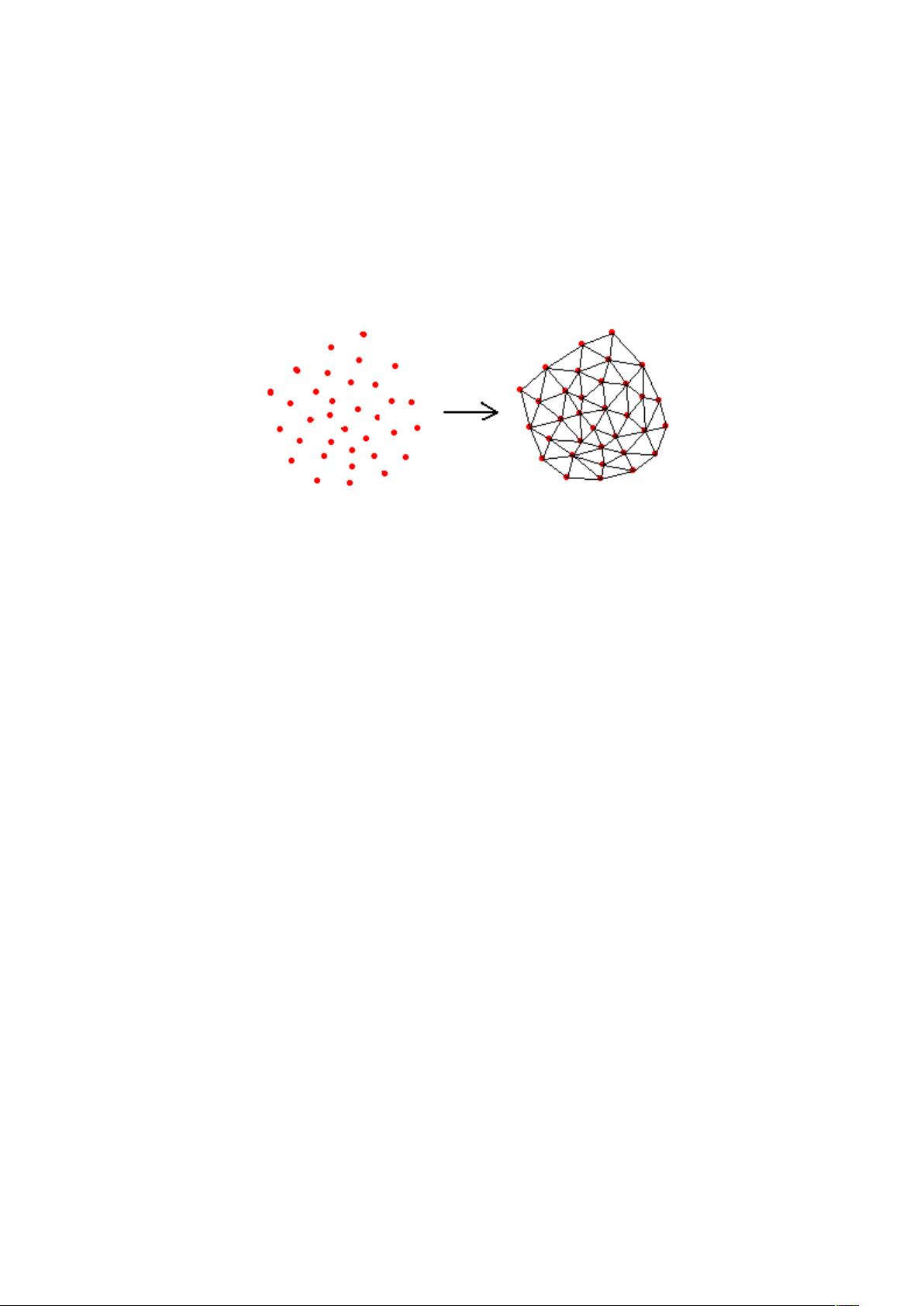
"本文介绍了Delaunay三角剖分的概念及其重要性，包括定义、准则和特性。Delaunay三角剖分是散点集的一种特殊三角化方式，具有空圆特性和最大化最小角特性，使得它在数值分析和图形学等领域广泛应用。" Delaunay三角剖分是一种在二维空间中将点集分割成一系列互不相交的三角形的几何构造，它是散点集三角化的一种重要方法。这种剖分的特点在于其满足特定的规则，使得在生成的三角形网络中，每个三角形的外接圆内不含除其顶点之外的任何点，这一特性被称为空圆特性。这种特性保证了三角剖分的内在质量，因为它避免了点过于紧密排列导致的细小三角形。 Delaunay边是满足空圆特性的边，即通过边的两个端点的圆内没有其他点。基于这些边构建的三角剖分就是Delaunay三角剖分。除了空圆特性，Delaunay三角剖分还遵循最大化最小角特性，意味着在所有可能的三角剖分中，Delaunay剖分形成的三角形具有最大的最小内角。这确保了三角形的相对规则性，有利于数值计算和图形渲染。 Delaunay三角剖分有以下几个关键特性： 1. 最接近性：Delaunay三角形由最近邻的三个点组成，避免了过长的边和细小的三角形，提高了数据表示的效率。 2. 唯一性：无论从哪个点开始构造，最终都会得到相同的Delaunay三角剖分，保证了算法的稳定性。 3. 最优性：在Delaunay三角网中，相邻三角形形成的凸四边形对角线互换后，不会导致最小内角增大，这保证了剖分的质量。 4. 最规则性：Delaunay三角剖分趋向于形成规则的三角形，减少了不规则形状，有利于后续处理。 在实际应用中，Delaunay三角剖分广泛用于地理信息系统、计算机图形学、有限元素分析等，例如在地形建模、图像渲染、模拟计算中，它可以提供稳定的网格结构，便于数据插值和计算。同时，Delaunay三角剖分也是构建voronoi图的基础，Voronoi图在各种领域都有应用，如地理信息系统中的服务区划分、物理模拟中的碰撞检测等。 实现Delaunay三角剖分的算法有多种，如Bowyer-Watson算法、Flip算法等，这些算法在处理不同规模和复杂度的点集时有不同的效率和适用性。Delaunay三角剖分是点集几何处理中的重要工具，它的理论和应用价值不容忽视。