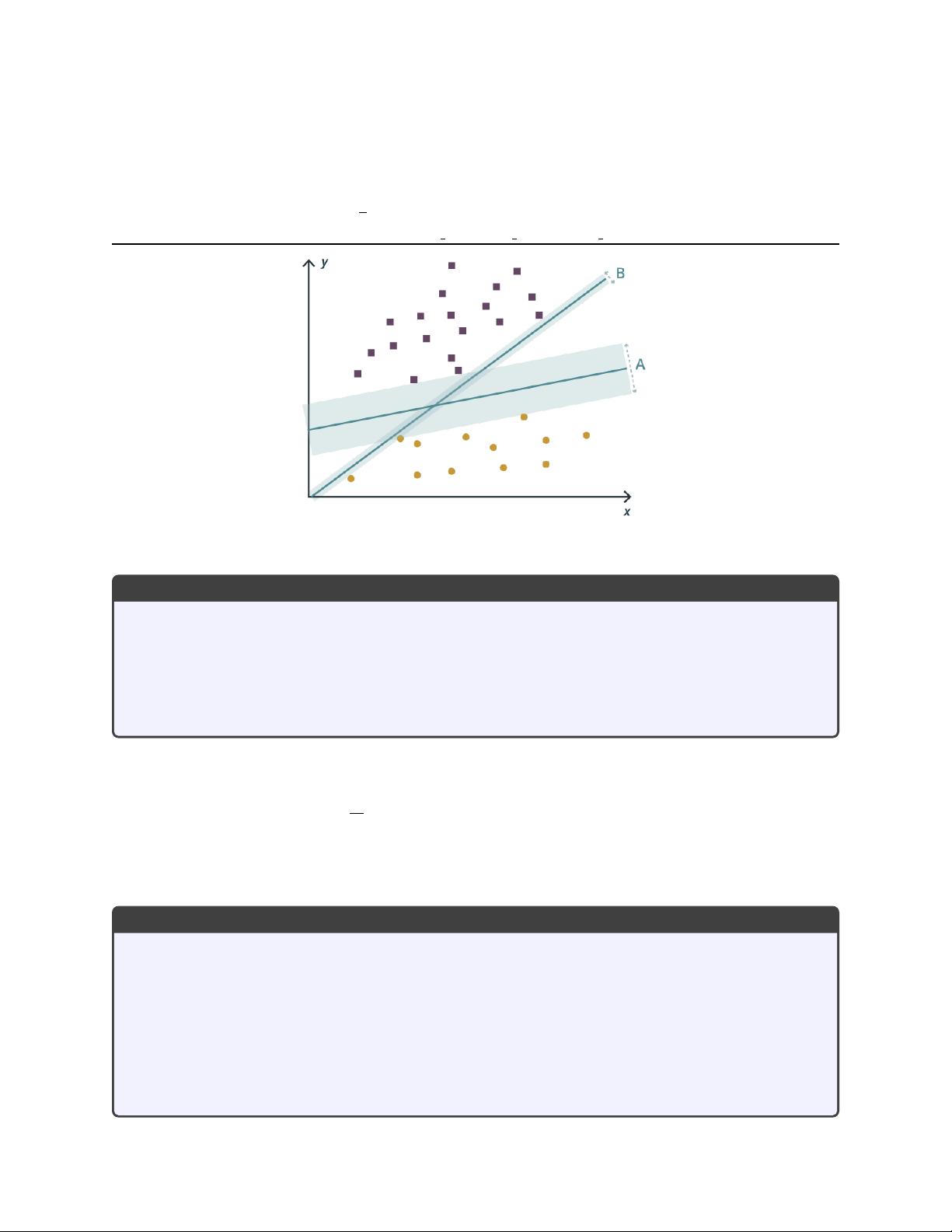
支持向量机与感知机：两种分类方法解析

"svm_lecture.pdf 是一份关于支持向量机（SVM）的讲座资料，探讨了在机器学习领域如何最大化两个数据集之间的分离。资料中提到了两种不同的分类方法，分别是逻辑回归和感知机问题，并介绍了线性可分的数据集概念。" 在机器学习领域，支持向量机（SVM）是一种强大的监督学习模型，主要用于分类和回归分析。它的工作原理是找到一个最优超平面，这个超平面能够最大程度地将不同类别的数据分开。在 SVM 中，我们不单纯追求最大间隔，而是寻找一个最大边距超平面，使得两类样本距离该超平面的最短距离最大，从而增加模型的泛化能力。 首先，资料中提到了一般超平面分离问题。给定n维数据点 x，其中一部分属于集合 P，目标是找到一组权重 w，使 y(xi) 能够指示 x 是否属于集合 P。超平面的方程可以表示为 y(xi) = w0 + Σ(wj * xi,j)，其中 w0 是偏置项，wj 是特征权重，xi,j 是数据点的第 j 个特征。 接着，资料对比了逻辑回归问题。在逻辑回归中，我们寻找最小化成本函数 J(w) 的权重 w，该成本函数是交叉熵损失函数，用于衡量预测概率与真实标签之间的差异。这与 SVM 的目标不同，SVM 直接优化的是间隔而不是误差。 然后，资料引出了感知机问题。感知机是一种简单的线性分类器，它试图找到一个超平面，使得正负两类样本被正确地分开，即正类样本的预测值大于零，负类样本的预测值小于零。对于线性可分数据集，感知机算法可以找到一个满足条件的解，但在非线性数据集上可能无法找到解决方案。 支持向量机的创新之处在于引入了核函数，它能将原始数据映射到高维空间，使得原本在低维空间中非线性可分的数据在高维空间中变得线性可分。常见的核函数有线性核、多项式核、高斯核（RBF）等，通过选择合适的核函数，SVM 可以处理复杂的非线性分类问题。 最后，SVM 的优化目标是最大化间隔，同时考虑了误分类的惩罚，这是通过软间隔最大化实现的。在 SVM 中，引入了松弛变量和惩罚项，允许一定程度的误分类，但会相应增加成本。这样，SVM 不仅寻找最大间隔，还考虑了数据点到超平面的距离，使得模型更加鲁棒。 总结起来，SVM 是一种有效的分类工具，通过最大化间隔和选择适当的核函数，能够在高维空间中构建非线性决策边界，从而实现对复杂数据集的精确分类。相较于逻辑回归和感知机，SVM 在处理非线性问题和避免过拟合方面表现出色。