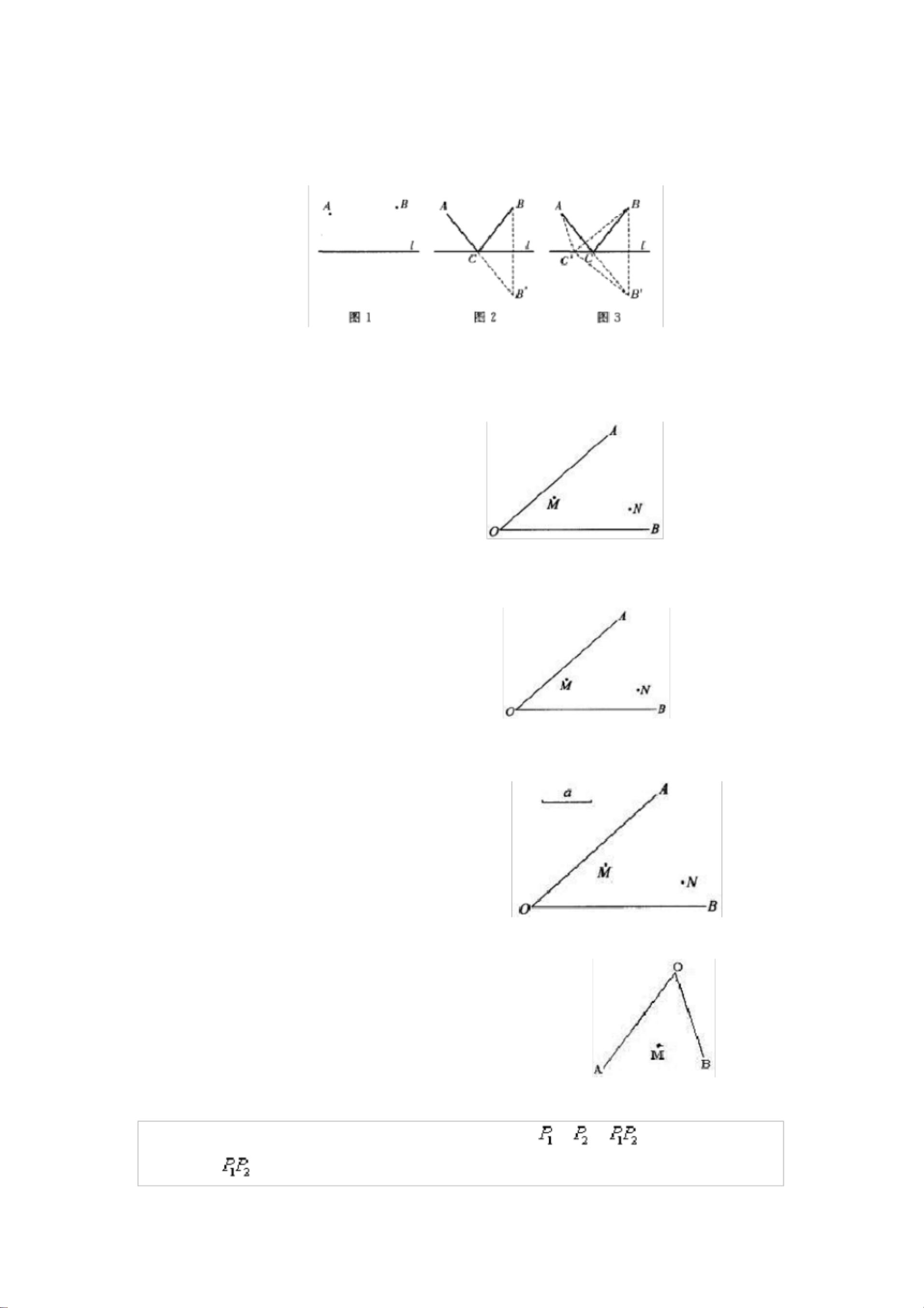
将军饮马问题：最短路径策略

"将军饮马问题" 将军饮马问题是一个经典的数学问题，源自中国古代的军事策略，涉及到几何学中的最优化路径选择。该问题的基本模式是：将军需要从起点出发，经过两个特定点（通常是河流），然后再返回起点，目标是最短化整个行程的总距离。在变式中，可能只需要经过一个返回点。 1. 基本模式：将军从马棚M出发，先到OA上的点P喝水，再到OB上的点Q喝水，最后返回校场N。求解这个问题的关键是找到点P和Q的位置，使得MP+PQ+QN的和最小。这通常可以通过构造相似三角形或者利用费马点的性质来解决。 2. 变式：在这种情况下，将军只需要从M到P，再到Q，不需要返回N。这时的目标是最小化MP+PQ。解法可能涉及寻找垂线段或通过轴对称变换找到最短路径。 3. 检阅队伍问题：将军要从M出发，先到P检阅队伍头，再到Q检阅队伍尾，最后返回N。最优解可能需要考虑P和Q同时满足将军检阅队伍和行走距离最短的条件。 4. 在OB边上找点P，使得PM+PO的和最小。这个问题可以通过构造最小值问题，如使用勾股定理和垂线段最短的原理来解决。 5. P关于OM，ON的对称点分别是P1和P2，若P1A=P2B=15，那么△PAB的周长为15+15，即30。这涉及到了对称性和线段长度的计算。 6. 找到∠AOB内的一点P，使得P到OA，OB的距离相等，同时到M，N两点的距离也相等。这样的点P是∠AOB的内心，它平分每个角并且与每条边垂直距离相等。 7. 当△PAB的周长取最小值时，问题转化为求解P到AB的最近距离。这可能涉及到构造平行线和利用相似三角形的性质。 8. 在四边形ABCD中，找到BP上的点P，使得DP的长度最小。这通常需要分析角的关系和应用勾股定理来找到最佳位置。 练习题： 1. 探究是否存在一个定点，使得点P与点A，B的距离总相等。这可能涉及到圆的定义，即圆上的所有点到圆心的距离都相等。 2. 建立货物中转站的问题是一个实际应用的最优化问题，中转站应建在两仓库距离之和的中点处，以达到最短总距离。 3. 在直线l的同侧找点P，使得PA+PB的和最小。这可以通过作垂线段来解决，因为垂线段是两条平行线间最短的线段。 4. 正方形中的问题未给出完整信息，但可能涉及到寻找正方形内的某点，使得该点到边界的某个点的距离最小。 以上问题的解决通常需要用到几何学中的概念，如相似三角形、轴对称变换、内心的性质、垂线段最短等，同时也可能需要利用代数方法进行求解。在处理这类问题时，理解几何图形，熟练掌握基本定理和性质是至关重要的。