遗传算法：生物进化与优化搜索的数学仿真

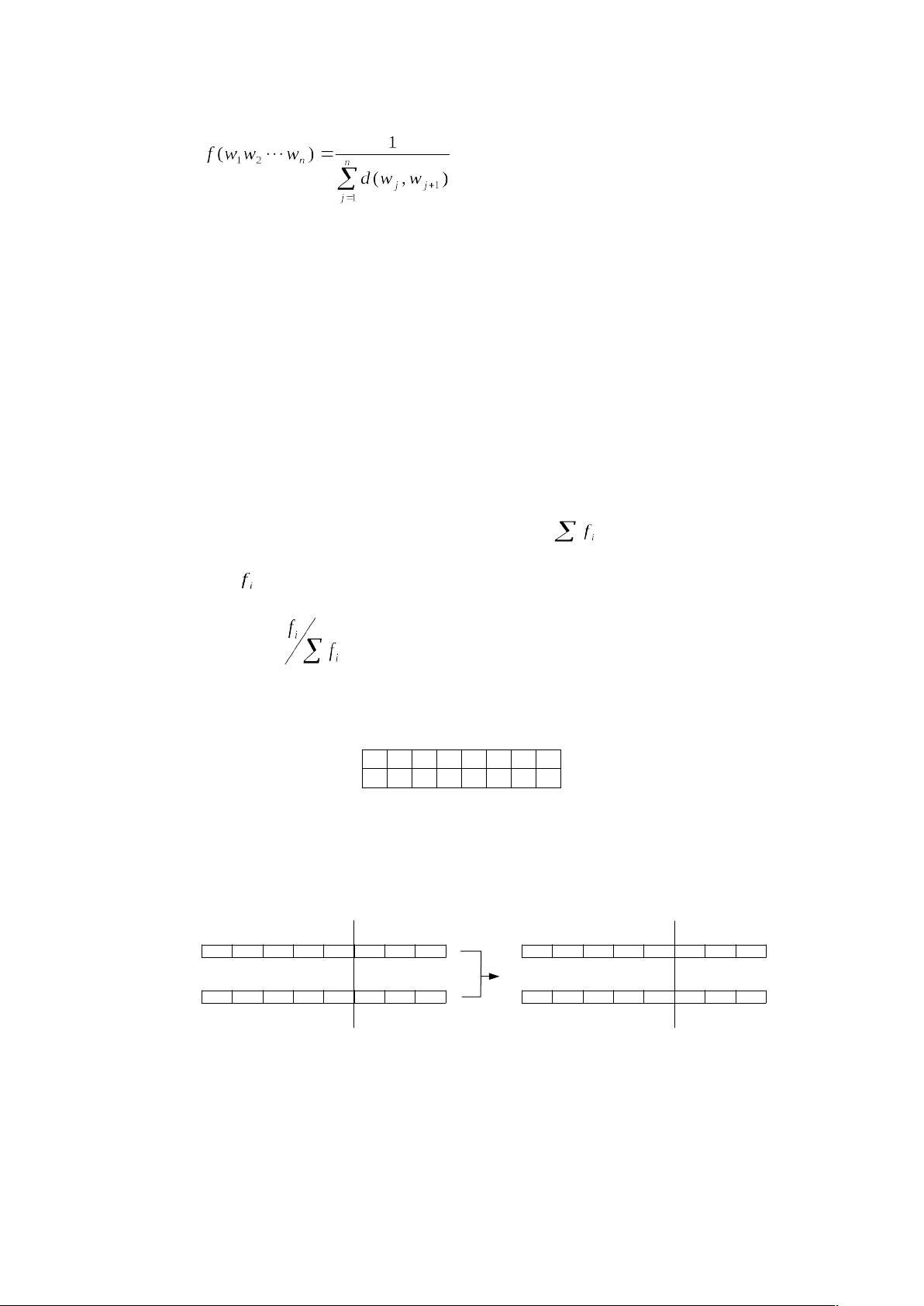
"本文档详细介绍了遗传算法的概念、原理及其在优化问题中的应用，特别是针对推销员旅行问题的实例解析。遗传算法作为一种模仿生物遗传学和自然选择机理的优化搜索算法，是进化计算的重要组成部分，它为解决复杂优化问题提供了新的思路。" 遗传算法是一种受到生物进化理论启发的计算方法，主要基于达尔文的物竞天择理论，通过模拟种群的进化过程来寻找最优解决方案。在遗传算法中，问题的可能解被抽象为"个体"，每个个体由一组参数或特征（即"基因"）组成，这些基因组合成"染色体"。染色体的适应度值用于衡量其对问题的适合程度，即解决问题的能力。 在遗传算法的执行过程中，首先创建一个初始的随机种群。然后，通过以下三个核心操作进行迭代优化： 1. **选择（Selection）**：根据适应度值，按照一定的概率选择一部分个体进行繁殖，强适应度的个体有更高的概率被选中，这是"适者生存"原则的体现。 2. **交叉（Crossover）**：被选中的个体进行基因重组，产生新的个体。交叉操作模拟生物的交配过程，通常采用单点、多点或均匀交叉等方式。 3. **变异（Mutation）**：在新生成的个体中，随机地改变部分基因值，以保持种群的多样性，防止过早收敛到局部最优解。 遗传算法在解决复杂优化问题时，不需要预先构建精确的数学模型，尤其适用于非线性、多目标、约束条件复杂等问题。推销员旅行问题（TSP）是一个经典的遗传算法应用案例。在这个问题中，遗传算法的目标是找到一条访问所有城市的最短路径，每对城市之间都有一个距离值。通过遗传算法，可以生成一系列可能的路径，经过多次迭代，逐步逼近最优解。 自霍兰德在1975年提出遗传算法以来，这个领域经历了近30年的发展，现在已经十分成熟，并广泛应用于工程优化、机器学习、网络路由、调度问题等多个领域。尽管遗传算法在解决某些问题时表现出色，但也有其局限性，如可能会陷入局部最优、计算量大等。因此，在实际应用中，往往需要结合其他优化技术，如模拟退火、粒子群优化等，以提高搜索效率和解的质量。 遗传算法以其独特的优化机制，为复杂问题的求解提供了一种有效的工具，体现了人工智能跨学科的融合创新。通过不断的研究和改进，遗传算法将持续在解决实际问题中发挥重要作用。