YANG et al.: RANDOM-FREQUENCY SAR IMAGING BASED ON COMPRESSED SENSING 985
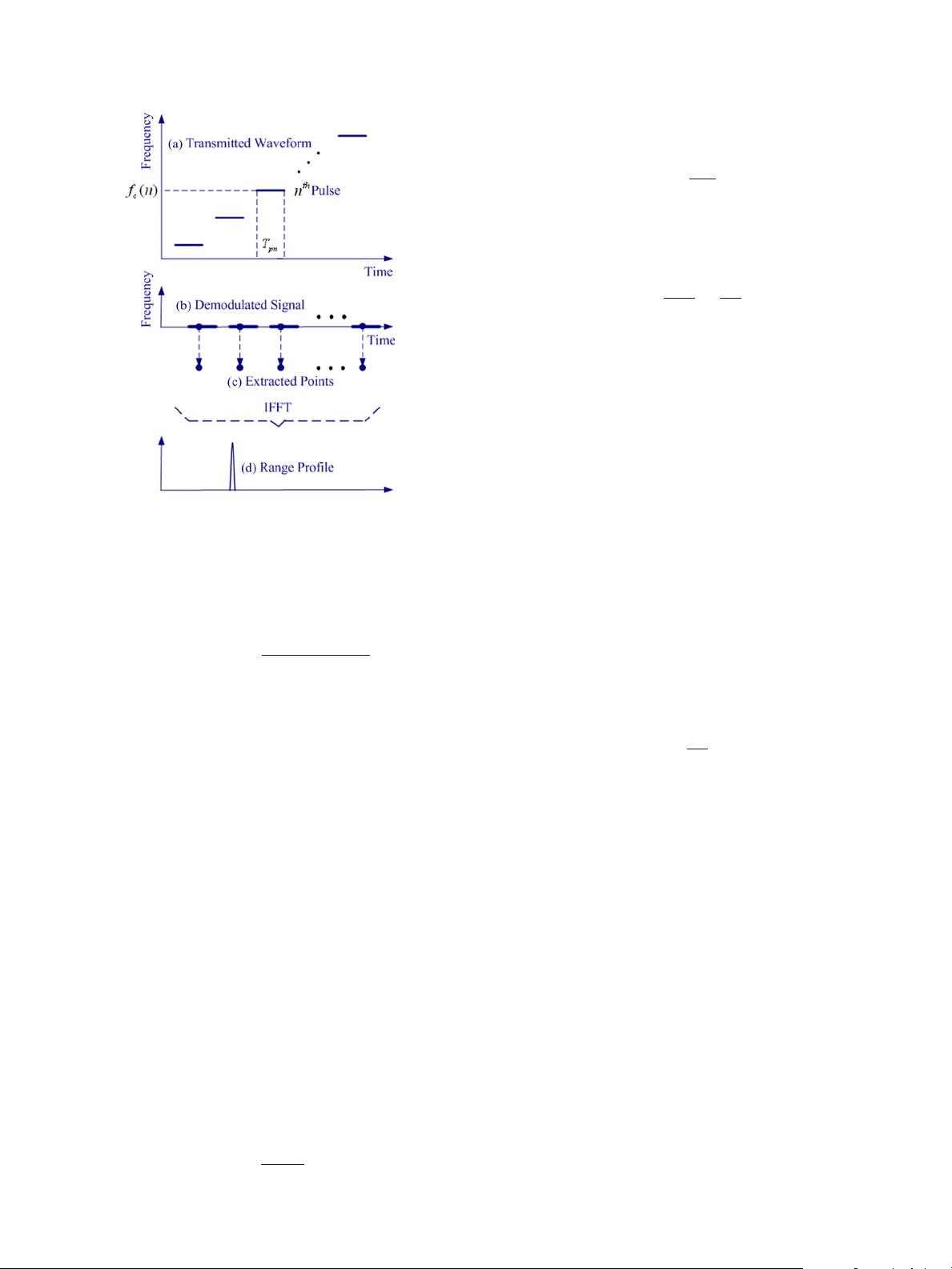
Fig. 1. Processing of stepped-frequency waveform. (a) Transmitted wave-
form. (b) Demodulated signal. (c) Extracted data points. (d) Range profile.
time window of each pulse and perform the IFFT to realize
range compression. The extracted sampling points before the
IFFT are
s(n)=g · exp
−j
4π(f
c
+Δfn)R
c
. (7)
The processing of the stepped-frequency waveform to obtain
the range profile is shown in Fig. 1. In the aforementioned
analysis, we assume that the target is stationary or nearly
stationary in the transmitting time of a sequence of frequencies.
If the target has a significant velocity, this assumption is not
valid. In this case, the target velocity will influence the range
profile [1], [2]. In [1], an algorithm is proposed that exploits
fully polarimetric data in order to improve the target radial
motion compensation. In [4], a compensation method for the
range difference of each frequency is proposed in the case of
SAR imaging. However, in the imaging scheme proposed in
this paper, this problem does not exist, since the sensing matrix
can be designed to match the range of each frequency exactly.
B. Limitations of Stepped-Frequency Waveform
Applied to SAR
We will now analyze the limitations of the stepped-frequency
waveform applied to SAR. The stepped frequency is discrete
in the frequency domain. This results in periodic repetition
in the time domain, and the repetition period is 1/Δf .The
corresponding repetition period for range is c/(2Δf),sothe
nonaliasing range width is limited to
R
w
<
c
(2Δf)
(8)
where R
w
denotes the nonaliasing range width.
For a fixed pulse time interval, to avoid overlapping of the
echoes, the maximum range width is
D
1
=
Δtc
2
(9)
where Δt is the time interval of the pulses. According to (8),
for a given frequency step, the maximum nonaliasing range
width is
D
2
=
c
2Δf
=
Nc
2B
(10)
where B is the signal bandwidth, and
B = NΔf. (11)
Therefore, the maximum available range width is
D =min{D
1
,D
2
}. (12)
In stepped-frequency SAR, the equivalent azimuth sampling
interval is NΔtV , where V is the radar velocity. To avoid
azimuth aliasing, the azimuth resolution will not exceed the
azimuth sampling interval, so that the upper limit of the azimuth
resolution is
r
a
= NΔtV. (13)
It should be noted that (13) is the upper limit of the azimuth
resolution restricted by the stepped-frequency parameters.
The actual azimuth resolution is determined by the synthetic
aperture length.
The range resolution is
r
r
=
c
2B
. (14)
From (8)–(14), we can see that the available imaging range
width and the range resolution and azimuth resolution must be
traded off against each other. To let the available range width
become wider, Δt and N should be bigger, B should be smaller,
but all of these requirements will decrease the resolution in both
the range and azimuth dimensions. The available imaging range
width is usually very narrow, unless the range and azimuth
resolutions are both significantly decreased. For instance, let
B = 512 MHz, N = 1536, V =50m/s, and Δt =3.2552 μs.
From the aforementioned parameters, we can calculate that
D
1
= 488.3 m, D
2
= 450 m, r
a
=0.25 m, and r
r
=0.293 m.
The available range width is only 450 m. If V increases, the
available range width will be reduced. If the platform velocity
V is smaller, the stepped-frequency SAR can obtain a higher
resolution while maintaining a wider range width. This implies
that the stepped-frequency SAR is most suitable for low veloc-
ity platforms.
Most of the aforementioned limitations are based on the
traditional sampling theory and will limit the application of the
stepped-frequency waveform in SAR. In the next section, we
will present a novel imaging scheme based on the CS theory.
The aforementioned limitations can be overcome if the targets
are sparse or compressible, so that the available imaging range









