982 Li
where the instantaneous phase
ˆ
8
m
(t) follows
ˆ
8
m
(t) = (m + 1)
µ
Z
t
0
ˆ
f (τ )dτ
¶
= (m + 1)
µ
f
L
t +
( f
H
− f
L
)t
2
2T
¶
, (7)
and the instantaneous frequency
ˆ
f
m
(t) is given by
ˆ
f
m
(t) = (m+1)
ˆ
f (t) = (m +1)
µ
f
L
+
( f
H
− f
L
)t
T
¶
. (8)
Theenvelope a
m
(t)inequation (6)issimilar toa
0
(t)[seeequa-
tion (2)] with c
0
being substituted by c
m
> 0.
Aharmonically distortedsweep (HDS) s(t)can bemodeled
as a sum of the fundamental sweep s
0
(t) and all its harmonic
distortions s
m
(t)
s(t) =
M
X
m=0
s
m
(t) =
M
X
m=0
a
m
(t)e
i2π
ˆ
8
m
(t)
, (9)
where M is the number of the harmonic distortions present
in the HDS s(t). At the recording geophone the fundamental
sweep s
0
(t) and all its harmonics s
m
(t) are superimposed, so
thattheycannotbeseparatedinthetimedomain.However,the
definition(8)impliesthat theinstantaneousfrequency
ˆ
f inthe
mth harmonic s
m
(t) changes linearly in the range (m + 1) f
L
≤
ˆ
f (t) ≤ (m + 1) f
H
and is assigned to the time
t
m
(
ˆ
f ) =
[
ˆ
f /(m + 1) − f
L
]T
f
H
− f
L
(m = 0, 1, 2,...,M).
(10)
Obviously
t
m+1
(
ˆ
f )< t
m
(
ˆ
f )(m=0,1,2,...,M). (11)
Thismeansthatthetimeoftheoccurrenceofthe(m + 1)thhar-
monic for a fixed instantaneous frequency
ˆ
f is always smaller
than that of the mth, and the time of any higher harmonic is
smallerthanthetimeofthefundamentalsweep.BoththePPSF
and the MFT, as it will be demonstrated in the following, fully
exploit thisinteresting timerelationship in the frequency-time
domain.
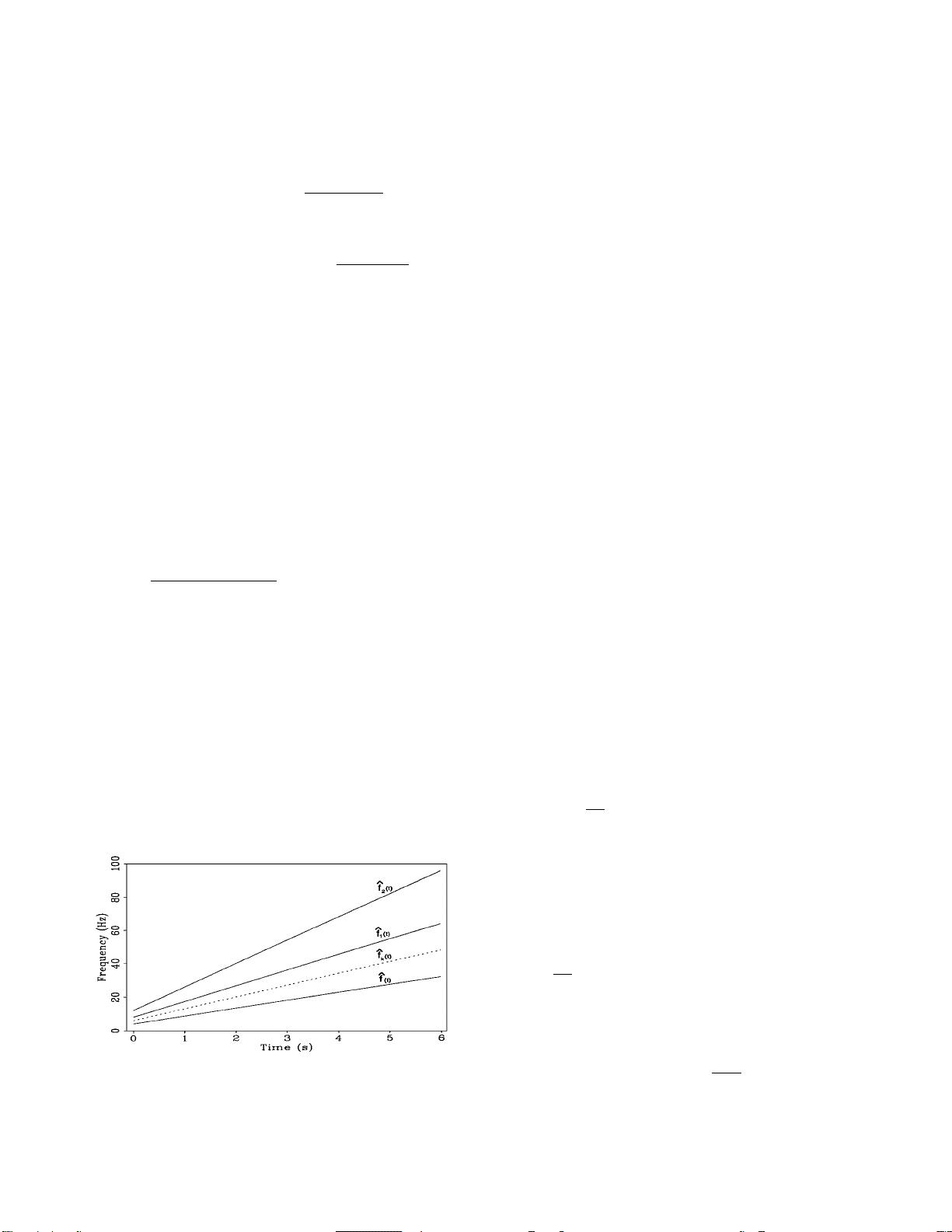
Figure1demonstrates the relationbetweenthearrivaltimes
of the fundamental sweep s
0
(t) and its harmonic components
s
m
(t)(m=1, 2)wherethe theoreticalfundamental sweeps
0
(t)
FIG.1. Therelationbetweentheinstantaneousfrequenciesand
the arrival times of the fundamental sweep s
0
(t) and its har-
monics s
m
(t)(m=1,2). Dashed line represents
ˆ
f
k
(t)ofthe
hypothetical kth (k = 0.5) harmonic distortion used for elimi-
nating harmonic distortion.
is computed with starting frequency f
L
= 4 Hz and end fre-
quency f
H
= 32 Hz. The duration of the sweep is T = 6s.Ac-
cordingtoequation(10)theoccurringtimest
m
(
ˆ
f )(m =0, 1, 2)
for the s
0
(t), s
1
(t), and s
3
(t) are, e.g., 3.43s, 1.29 s, and 0.57 s in
the caseof afrequency
ˆ
f = 20 Hz. The dashedline in Figure 1
represents the “kth harmonic distortion” (k = 0.5) used for
computing thePPSF (Liet al., 1995). Itwill beobserved in the
following decomposition (see Figure 5) that the energy of the
fundamental sweep and its harmonic components distributes
along these time-frequency relations
ˆ
f
m
(t)(m=0, 1, 2)in the
(F–t)-domain. The same is valid for the “kth harmonic distor-
tion” (dashed line). If a negative time shift is done, e.g., by t
k
(for
ˆ
f = 20Hz,−t
k
|
k=0.5
=−2.00s),whichistheoccurringtime
of thehypothetical “kth harmonic distortion” for theinstanta-
neous frequency
ˆ
f defined by equation (10), all energy of all
mth(m > 0)harmonicdistortionsisshiftedtothenegativetime
domain. By taking only the energy of the fundamental sweep,
whichliesin thepositivetime domain, onecan easilyeliminate
any higher harmonic distortions. After the amplitudes in the
negativetimedomainare settozero,the fundamental sweepis
shiftedbacktoitsoriginaltimewiththesamepositivetimeshift
t
k
.In practice, thiselimination processis doneinthe frequency
domain with the help of the PPSF. Details of eliminating the
harmonic distortion of the vibroseis data by using the PPSF
can be found in (Li et al., 1995).
MULTIPLE FILTER TECHNIQUE
The decomposition of the HDS s(t) in equation (9) is
achieved for each selected vibroseis signal by Fourier trans-
form and Gaussian filtering, followed by computing the en-
velope trace and the measurement of the envelope amplitude
along the instantaneous frequency
ˆ
f
m
(t)(m=0,1,2,...,M)
in the (F–t) domain.
Fouriertransform.—Eachharmoniccomponents
m
(t)canbe
given by the following Fourier-integral pair
S
m
(ω) =
Z
∞
−∞
s
m
(t)e
−iωt
dt =|S
m
(ω)|e
−i8
m
(ω)
, (12)
s
m
(t) =
1
2π
Z
∞
−∞
S
m
(ω)e
iωt
dω = a
m
(t)e
i2π
ˆ
8
m
(t)
m = 0, 1, 2,...,M, (13)
and a similar Fourier-integral pair exists for the HDS s(t)
S(ω) =
Z
∞
−∞
s(t)e
−iωt
dt =
M
X
m=0
|S
m
(ω)|e
−8
m
(ω)
, (14)
s(t) =
1
2π
Z
∞
−∞
S(ω)e
iωt
dω =
M
X
m=0
a
m
(t)e
i2π
ˆ
8
m
(t)
. (15)
Gaussian filtering.—To carry out the decomposition, the
Gaussian filter G(ω, ω
n
) (Dziewonski et al., 1969)
G(ω, ω
n
) = e
−η
³
ω−ω
n
ω
n
´
2
(16)
isused,whereω
n
= 2π f
n
isavariablecenterangularfrequency
ofthefilterG(ω, ω
n
),andη isaparametercontrollingtheshape
Downloaded 03 Aug 2009 to 60.214.232.41. Redistribution subject to SEG license or copyright; see Terms of Use at http://segdl.org/









