线性优化的灵敏度分析

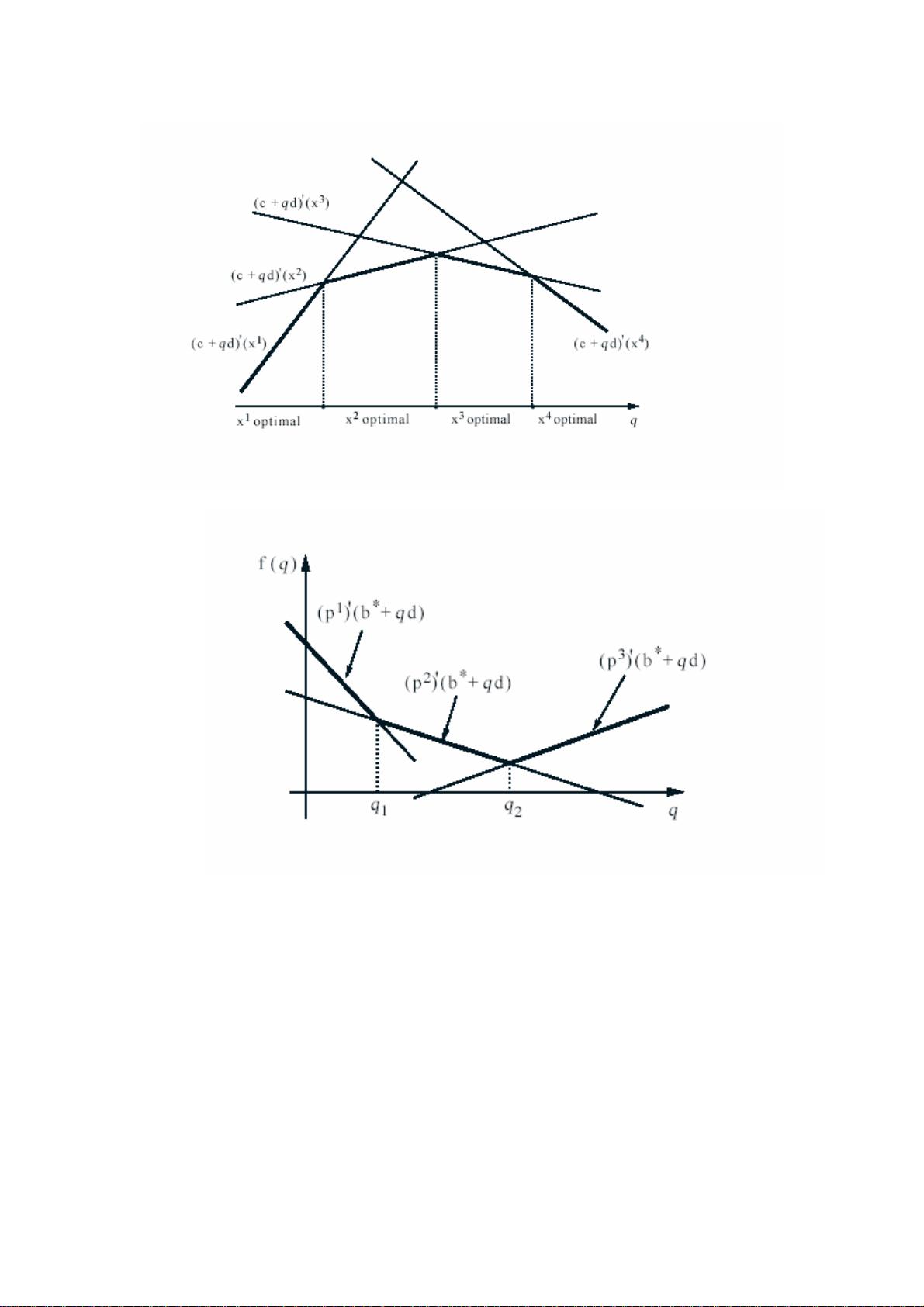
"这篇文档主要介绍了灵敏度分析在最优化方法中的应用，特别是线性优化问题。内容包括全局灵敏度分析和局部灵敏度分析，并通过具体的例子解释了这些概念。" 在最优化问题中，灵敏度分析是一个关键的工具，用于理解模型参数变化对解决方案的影响。这份资料详细阐述了这个主题，主要分为两个部分：全局灵敏度分析和局部灵敏度分析。 1. 全局灵敏度分析： - 当我们改变目标函数中的系数c或者约束条件的右端常数b时，全局灵敏度分析研究的是这些变化如何影响优化问题的解。例如，如果c增大，目标函数的价值可能会增加或减少，这取决于c对应的变量是在当前解中是正的还是负的。 - 全局灵敏度分析也涉及原函数与对偶函数之间的关系。在这里，原问题是最大化或最小化某个目标函数，而对偶问题则是寻找一个最优解，使得原问题的边界条件得到满足。当b改变时，原函数的凸函数性质和对偶函数的凹函数性质对于理解解的稳定性至关重要。 2. 局部灵敏度分析： - 局部灵敏度分析更关注于微小变化对当前最优解的影响。例如，如果资源数量b中的某个元素b_i发生变化，我们需要检查新的解是否仍然最优。 - 在局部灵敏度分析中，基B的最优性需要满足两个条件：可行性条件（所有约束均满足）和最优性条件（KKT条件）。如果b_i发生变化，我们需要重新检查这两个条件，以确认基B是否保持最优。 3. 实际应用： - 通过灵敏度分析，我们可以发现哪些参数的变化对最终决策影响最大，这对于管理决策、资源分配以及风险评估等实际问题具有重要意义。例如，在供应链管理中，了解价格变化如何影响利润是最优订货量，或者在工程设计中，分析材料成本变动如何影响总成本。 灵敏度分析提供了一种量化理解模型参数变化如何影响优化问题解的方法，这对于理解和预测复杂系统的行为，以及在不确定环境中做出稳健决策至关重要。无论是全局还是局部的分析，都可以帮助我们在实际问题中找到更稳定、更适应变化的解决方案。