Mathematica中的多项式运算与方程求解

本章节主要探讨的是Mathematica软件中的基本运算，特别是针对多项式的处理。多项式在数学中是一种重要的代数结构，它允许我们进行诸如加法、减法、乘法和除法等运算。在Mathematica中，提供了丰富的内置函数来操作多项式，包括： 1. **多项式表示与展开**: - `Expand[]`: 展开多项式，如`Expand[x^8 - 1]`分解为`(x^4 - 1)(x^4 + 1)`。 - `ExpandAll[]`: 全部展开多项式，确保所有可能的项都出现。 - `Factor[]`: 对多项式进行因式分解，如`Factor[x^8 - 1]`。 - `FactorTerms[]`: 按指定变量分解，如`FactorTerms[poly, {x, y}]`。 2. **简化与收集项**: - `Simplify[]`: 将多项式化简到最简形式，如`Simplify[(2 + x)^4 (1 + x)^4 (3 + x)^3]`。 - `FullSimplify[]`: 展开后进一步简化。 - `Collect[]`: 按指定变量的幂次展开多项式。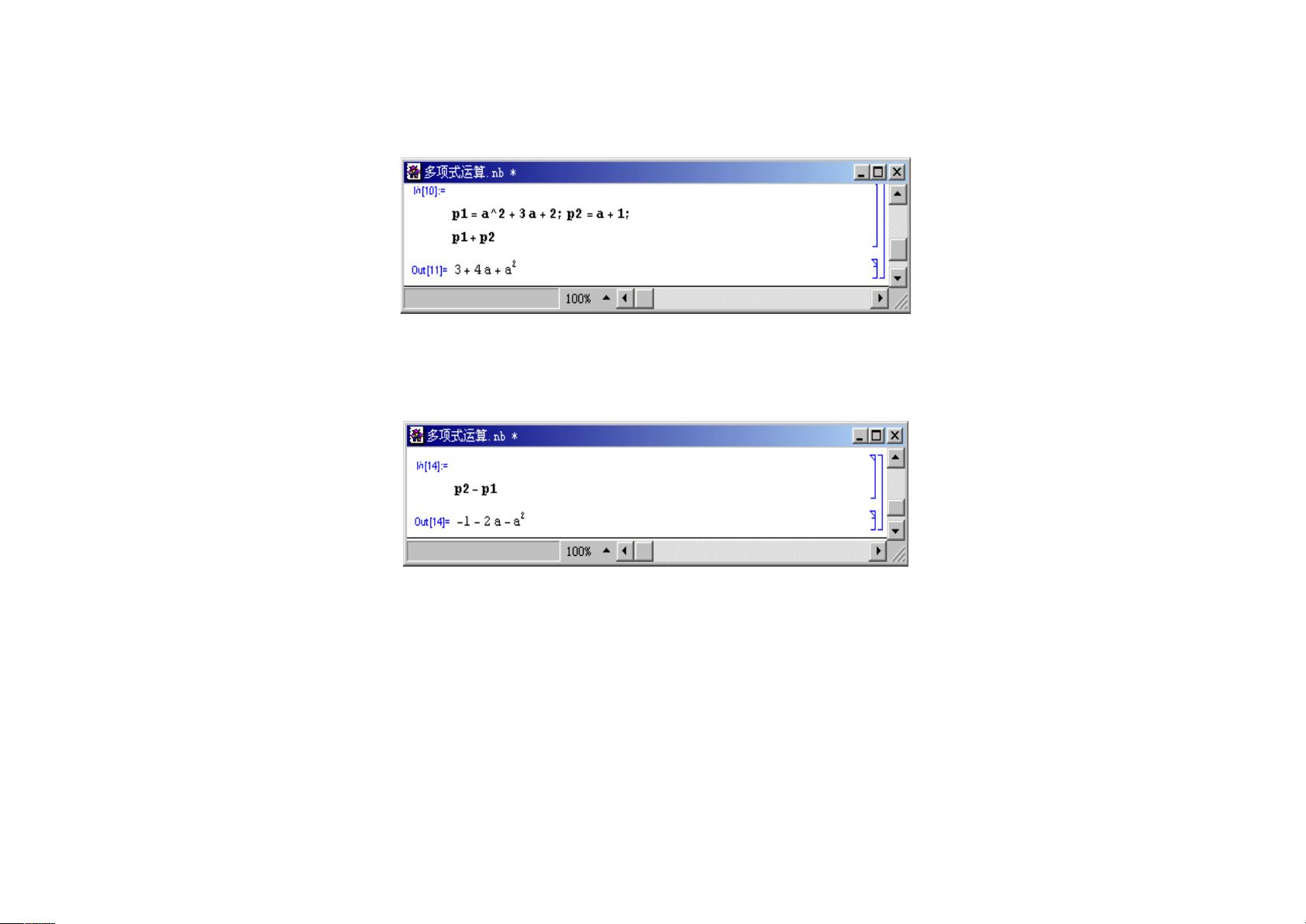 3. **多项式运算**: - 加法和减法：例如多项式`a2 + 3a + 2`与`a + 1`的加减运算。 - 乘法和除法：通过`*`和`/`符号进行，如`(1 + x)^5`的展开和多项式相乘、相除。 - `Cancel[]`: 可以约去多项式中的公因式。 4. **方程和根的表示**: Mathematica将方程视为逻辑语句，例如`x^2 - 2x + 1 = 0`。用户可以通过这些函数处理方程，虽然它们主要用于逻辑求解而非纯粹的数学表达。 通过这些函数，用户能够方便地进行多项式的各种操作，无论是基础的展开、分解，还是复杂的运算和简化，Mathematica都提供了强大的工具支持。这对于理解和解决数学问题，特别是在符号计算和数值计算中，是非常实用的。