Simulink仿真：单自由度阻尼系统与弹簧振动的微分方程研究

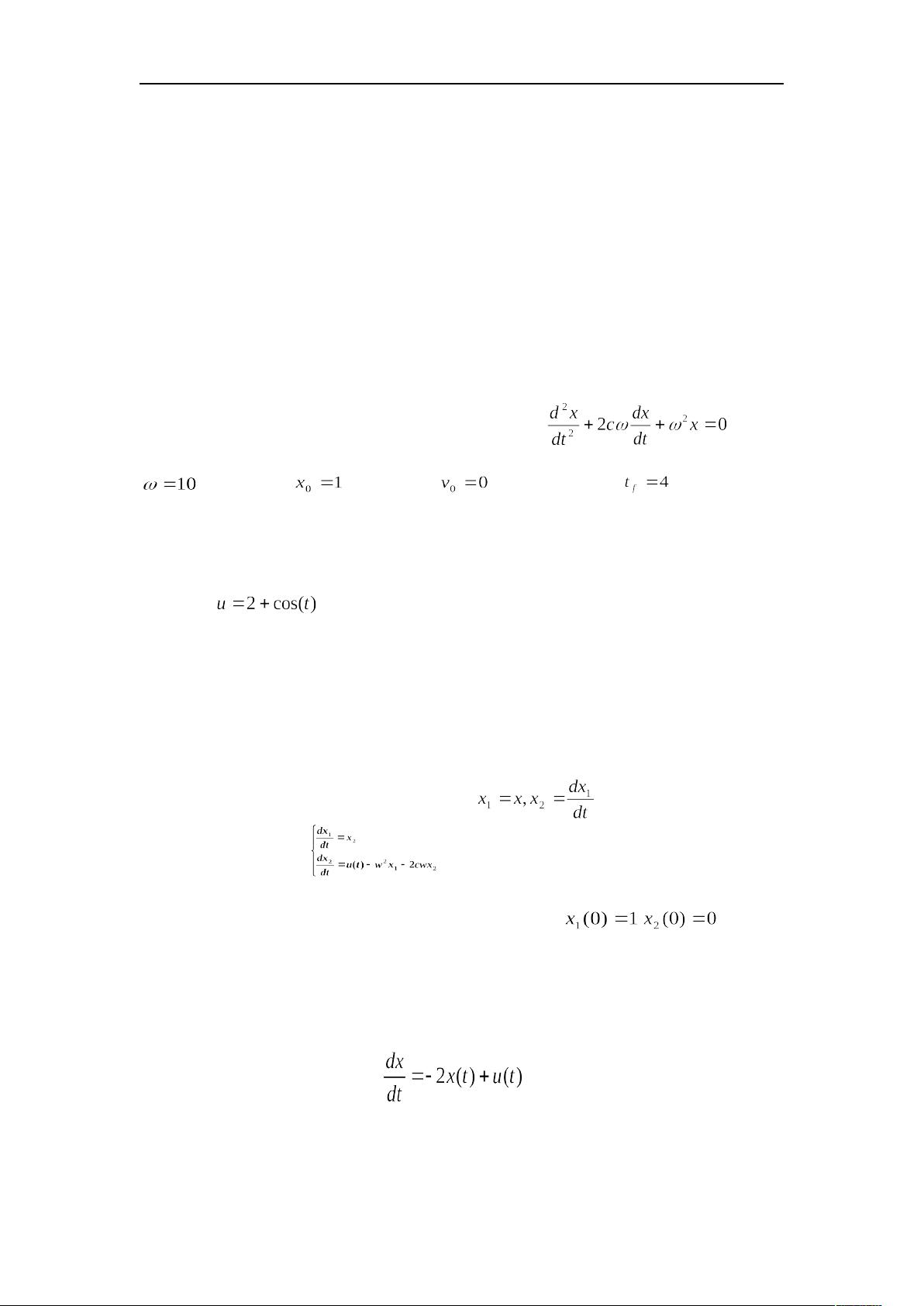
微分方程数值仿真实验主要围绕单自由度阻尼系统和弹簧振动的动态仿真展开，旨在通过实践提升学生对Simulink软件的运用能力和微分方程理论的理解。以下是关键知识点的详细阐述： 1. **单自由度阻尼系统仿真**： - 实验目标包括动态模拟单自由度系统，展示阻尼系数如何影响系统的振动行为。通过设置无强迫力的条件，固定初始位置和速度，确定终点时间，观察阻尼系数如何改变振动曲线的衰减程度，从而理解阻尼对系统固有模态的影响。 2. **弹簧振动仿真**： - 学生需要模拟弹簧振动的基本情况，比如一弹簧沿水平方向运动，其位移遵循特定的振动规律。通过运行exp2_3.m程序，可以看到弹簧振动的动画，直观感受不同阻尼系数下的响应特性。 3. **微分方程的ode指令**： - 学习如何使用ode指令（如ode45）求解微分方程，将高阶方程转化为一阶微分方程组，如将复杂数学模型简化为形式如[pic]的表达式。同时，理解初始条件的设定，如[pic][pic]。 4. **方程框图化和Simulink设计**： - 学生需学会将数学模型转化为Simulink中的方程框图，这是Simulink仿真的基础，它允许用户可视化并模拟复杂的系统动态。通过这个过程，学生可以初步掌握Simulink的结构和逻辑设计思路。 5. **实时动画编程原理**： - 在实验中，不仅涉及静态仿真，还涉及到实时动画的编程，让学生理解如何在Simulink中实现动态的视觉反馈，这有助于深入理解物理过程和算法执行的实际效果。 6. **知识背景与微分方程理论**： - 微分方程是描述物理系统动力学的基础工具。在汽车振动问题中，使用二阶线性微分方程描述了质量、弹簧和减震器组成的系统。阻尼系数、稳态增益和自然频率等参数在方程中起关键作用，它们反映了系统的固有性质。 通过本实验，学生将理论知识与实际应用相结合，提高解决实际问题的能力，并进一步巩固微分方程在工程领域中的核心地位。同时，对Simulink软件的熟练掌握也将为他们未来在控制工程、信号处理等领域的发展打下坚实的基础。