DBSCAN算法：基于密度的聚类

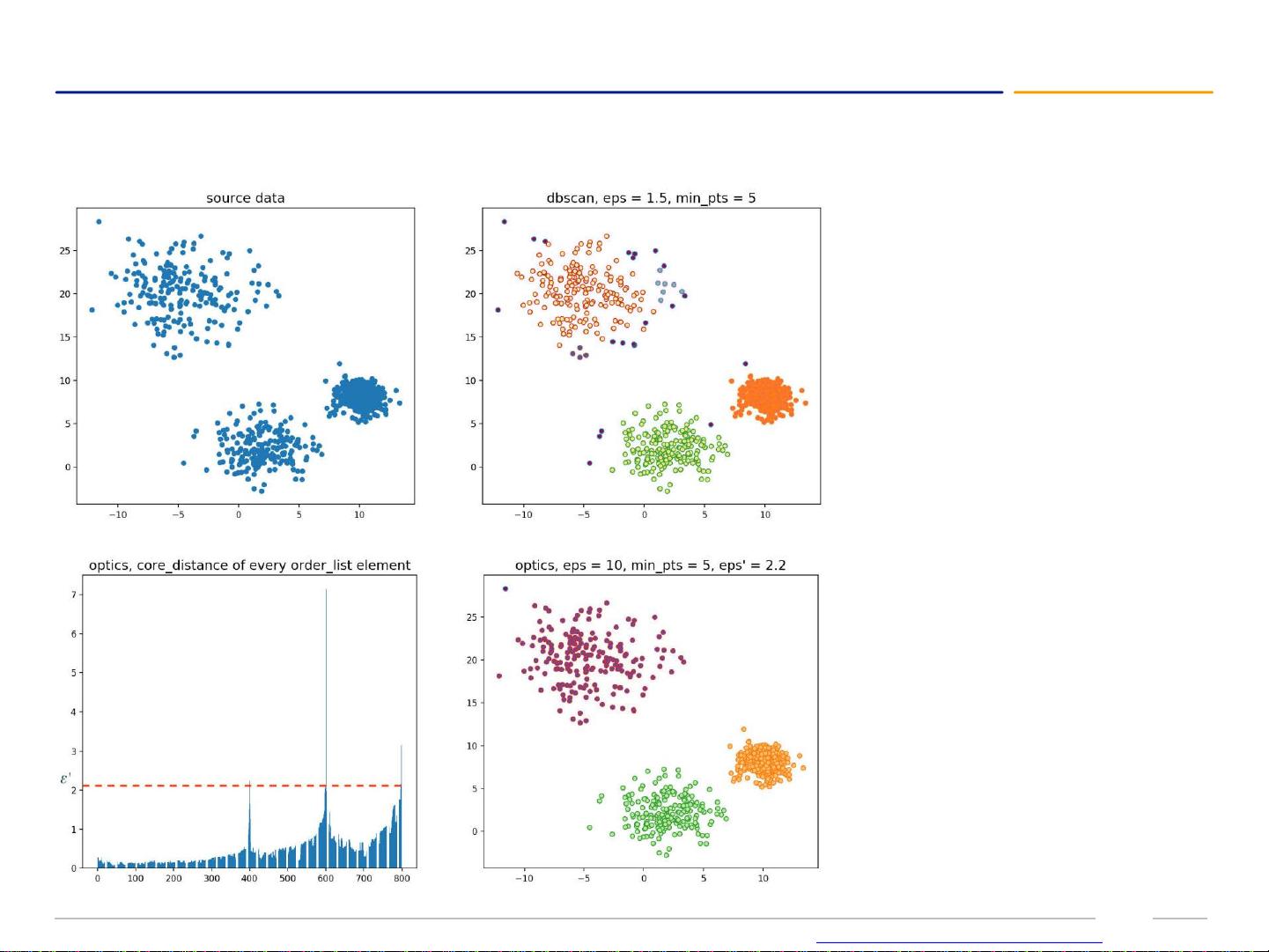
DBSCAN算法是一种基于密度的聚类算法，它通过使用关于"邻域"的参数来描述样本分布的紧密程度。该算法将数据点分为三类：核心点、边界点和噪音点。 核心点是指在半径为eps的邻域内含有超过min_pts个点的数据点。这意味着核心点周围的密度比较高，可以看作是簇的中心。边界点是指在半径为eps的邻域内点的数量小于min_pts，并且落在核心点的邻域内的点。这些点周围的密度较低，可能是簇的边界点。噪音点则既不是核心点也不是边界点，它们分布在簇外的孤立点。 DBSCAN算法的核心思想是通过计算数据点之间的距离来确定它们之间的相似性，进而进行聚类。与传统的聚类算法相比，DBSCAN算法不需要提前指定簇的数量，而是根据数据点之间的密度关系来自动确定簇的数量和形状。 在DBSCAN算法中，存在四种点的关系：密度直达、密度可达、密度相连和噪音点。 密度直达是指如果点P是核心点，点Q在P的半径为R的邻域内，那么可以说P到Q是密度直达的。密度直达满足一定的条件，即P到Q是直接可达的关系，但反过来不一定成立。 密度可达是指如果存在核心点P2、P3、...、Pn，且P1到P2是密度直达、P2到P3是密度直达，以此类推，那么可以说P1到Pn是密度可达的。密度可达关系可以看作是一条连接了多个密度直达关系的路径。 密度相连是指如果存在一个核心点P和两个点组成的路径，即P1到P2密度直达，P2到P3密度直达，那么可以说P1和P3是密度相连的。密度相连关系通过连接多个密度直达关系来构建更长的路径。 噪音点是指既不是核心点也不是边界点的点，它们与任何其他点之间都没有密度直达或密度可达的关系。 DBSCAN算法的优势在于它可以发现任意形状的簇，并能够将噪音点排除在外。它还可以根据关于邻域的参数来调整簇的密度，从而更好地适应不同的数据分布。 综上所述，DBSCAN算法是一种基于密度的聚类算法，通过计算数据点之间的距离和密度关系来确定簇的数量和形状。它将数据点分为核心点、边界点和噪音点，并能够发现任意形状的簇。该算法的应用领域广泛，包括图像分析、模式识别、航空航天等。