热退火中硅纳米晶形成模拟研究

57 浏览量更新于2024-08-27 收藏 204KB PDF 举报

"Modeling of silicon-nanocrystal formation in amorphous silicon/silicon dioxide multilayer structure" 本文深入探讨了在多层非晶硅/二氧化硅（a-Si/SiO2）结构中，纳米硅晶（Si-NCs）在热退火过程中的形成机制。研究基于吉布斯自由能变化的修改模型，该模型引入了平均有效界面自由能变化的概念，考虑了成核和随后生长的整体过程。在a-Si/SiO2多层结构中，当进行热处理时，纳米硅晶的形成是一个复杂的过程。通过理论计算，研究人员发现存在一个硅层厚度的下限，只有当硅层厚度超过这个阈值时，才能在a-Si/SiO2多层结构中形成Si-NCs。这意味着，如果硅层太薄，将无法支持纳米晶的稳定存在。此外，计算结果显示，氧化物界面并不能限制Si-NCs的横向生长，这暗示了在纳米尺度上，晶粒可能会跨越界面扩展。文章进一步对比了a-Si/SiO2和纯a-Si结构中纳米晶的形成情况。通常，二氧化硅的存在可以作为成核的促进剂，因为它可以提供一个不同的能量状态，有利于硅原子的聚集。在多层结构中，连续的a-Si和SiO2交替层可能为纳米晶的形成提供了更多的成核位点，增加了纳米晶的密度和均匀性。在热退火过程中，硅原子会经历从非晶态到晶态的转变，形成纳米晶。这一转变是通过能量的最小化完成的，其中吉布斯自由能的变化起着关键作用。平均有效界面自由能变化的概念帮助理解了在这个过程中能量如何在不同相之间分布，以及为什么在特定条件下纳米晶能够稳定形成。通过对整个形成过程的建模，研究者能够预测不同参数（如温度、硅层厚度、氧化物厚度等）对纳米晶尺寸、数量和分布的影响。这对于优化纳米晶硅基光电材料的性能，例如太阳能电池和光电子设备，具有重要的实际应用价值。这项工作揭示了在a-Si/SiO2多层结构中纳米硅晶形成的物理机制，并提供了设计和控制这些纳米结构的理论基础。未来的研究可能聚焦于如何精确控制纳米晶的尺寸和排列，以实现更高效、更稳定的纳米晶硅器件。

December 10, 2010 / Vol. 8, No. 12 / CHINESE OPTICS LETTERS 1199

Modeling of silicon-nanocrystal formation in amorphous

silicon/silicon dioxide multilayer structure

Keyong Chen (]]]), Xue Feng (¾¾¾ ÈÈÈ)

∗

, and Yidong Huang (ÀÀÀ)

State Key Laboratory of Integrated Optoelectronics, Department of Electronic Engineering,

Tsinghua University, Beijing 100084, China

∗

E-mail: x-feng@tsinghua.edu.cn

Received August 5, 2010

The formation process of silicon-nanocrystals (Si-NCs) in the amorphous silicon/silicon dioxide (a-Si/SiO

)

multilayer structure during thermal annealing is theoretically studied with a modiﬁed model based on the

Gibbs free energy variation. In this model, the concept of average eﬀective interfacial free energy variation

is introdu ced and the whole formation process consisting of nucleation and subsequent growth is considered.

The calculating results indicate that there is a lower limit of the silicon layer thickness for forming Si-NCs

in a-Si/SiO

multilayer, and the oxide interfaces cannot constrain their lateral growth. Furthermore, by

comparing the results for a-Si/SiO

and a-Si/SiN

multilayers, it is found that the constraint on the crystal

growth from the d ielectric interfaces depends on the diﬀerence between interfacial free energies.

OCIS codes: 310.0310, 310.6805.

doi: 10.3788/COL20100812.1199.

Eﬃcient silicon-based lig ht s ource is one of the most pop-

ular topics in the studies on silicon (Si) photonics that

has attracted many attentions due to its compatibility

with existing semiconductor fabrication techniques. For

this topic, various approaches have b een explored, such

as porous Si

[1,2]

and Si nanocrystals (Si-NCs) in bulk Si-

rich compounds

[3−5]

and multilayers

[6,7]

. Among them,

Si-NCs are holding the a ttention for their strong quan-

tum conﬁnement eﬀects with stable optical properties,

especially when multilayer structure is consider e d as a

method to independently regulate the size and density

of Si-NCs, and improve light emission with substantially

lower driving voltage

[6]

. Nevertheless, compared with

that in bulk Si-rich compounds

[8]

, the formation of Si-

NCs in ultrathin amorphous Si (a-Si) layers covered with

thin dielectric layers, such as SiO

and Si

, i.e., a-Si

multilayers, has not been widely studied. The existing

theories

[9,10]

cannot well clarify the whole formation pr o-

cess of Si-NCs in multilayers by modeling nucleation and

subsequent growth separately. In this letter, for bet-

ter understanding and control of the Si-NC formation,

a modiﬁed mo del is developed to unify the formation

process based on the Gibbs free energy variatio n. Ac-

cording to the calculations using the proposed model, a

lower limit for the a-Si layer thickness and incapability

of constraint on the lateral growth of Si-NCs from the

oxide interfaces are discovered in a-Si/SiO

multilayers.

Furthermore, the model could be readily applied to es-

timate the diﬀerences between interfacial free energies,

which correspond to diﬀerent dielectric materials. By

comparing the results of a-Si/SiO

and a-Si/SiN

multi-

layers, we ﬁnd that the constraint on the Si-NC growth

from the dielectric interfaces depends on the diﬀerence

between interfacial free energies.

In genera l, the formation of Si-NCs includes nucleation

and the following growth, induced either by furna ce

annealing or pulsed laser

[11]

. Nucleation occurs homoge-

neously in the interior of the uniform amorphous phase

or heterogeneously at preferential sites such as impuri-

ties, interfaces, and defects. After nucleation, Si-NCs

would grow up with suﬃcient external thermal energy.

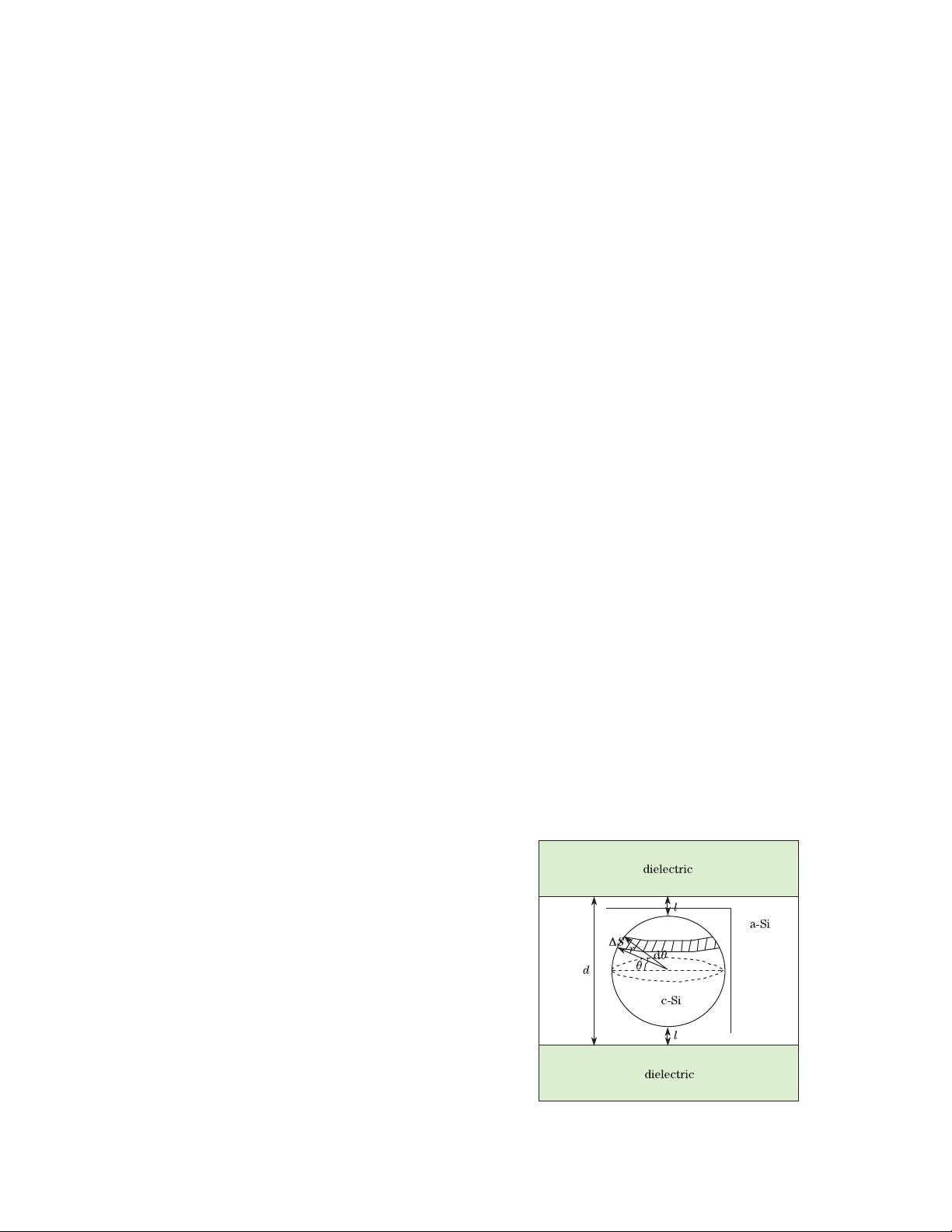
Here, we divide the whole formation process into two

successive stages, i.e., pre-touch and post-touch of the

dielectric interfaces. The multilayer is simpliﬁed as an

a-Si/dielectric sandwich structure as shown in Figs. 1

and 2. In the pre-touch stage, a Si-NC is assumed to

nucleate symmetrically in the middle of the a-Si layer

with spherical shape with radius r. As in Ref. [9],

spacing l is introduced to s e parate the cr ystal nucleus

from the dielectric interfaces. When the Si-NC keeps

growing up and intersects the top and bottom inter-

faces, the p ost-touch stage will begin. However, it will

be shap e d like a drum with lateral diameter beyond the

layer thickness d. Moreover, we deﬁne γ

as the inter-

facial free energy per unit area between the a-Si phase

and the crystalline Si (c-Si) phase, γ

as that between

the dielectric material and the c-Si phas e , and γ

that between the dielectric material and the a- Si phase.

According to the deductions in Ref. [9], we can then

achieve the eﬀective interfacial free energies γ

eﬀ

and γ

eﬀ

Fig. 1. Schematic diagram of the Si-NC in the pre-touch

stage.

1671-7694/2010/121199-04

 2010 Chinese Optics Letters

下载后可阅读完整内容，剩余3页未读，立即下载

weixin_38685857

粉丝: 5
资源: 890

热退火中硅纳米晶形成模拟研究

MODELING-OF-SILICON-CONTROLLED-RECTIFIER.rar_silicon_silicon con

Integrated System-Level Modeling of Network-on-Chip enabled Multi-Processor Platforms.pdf

Modeling-and-simulating-of-SVPWM-control-system-o_嵌入式/单片机/硬件编程_PDF_

AND-Gate-Using-Behavioral-Modeling---iblocks_file_VHDL/FPGA/Verilog_VHDL_

Finite element modeling of pore-fluid flow in the Dachang ore district, Guangxi, China: Implications for hydrothermal mineralization (2011年)

Modeling and simulation of the effect of surface roughness on properties of silicon-on-insulator optical ring resonator coupled with a straight waveguide

Modeling-wolf-population-in-the-Netherlands

Modeling-and-Simulation-in-Python-pdf.pdf.pdf

Modeling of open-coupled homogeneous striplines

Reliability and maintenance modeling of multi-state degraded systems

最新资源