提升效率：树状数组详解及其在编程中的应用

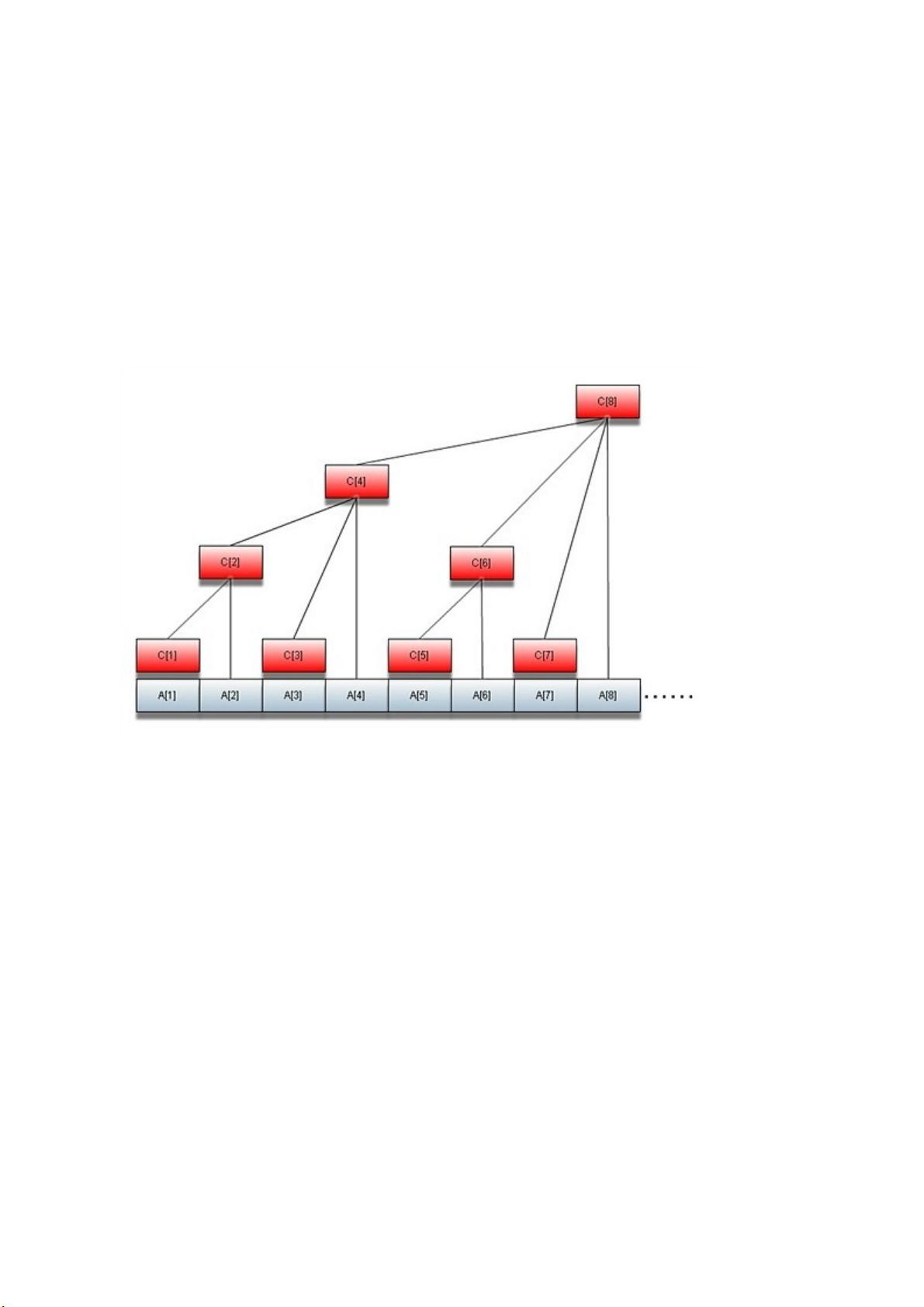
树状数组是一种高级数据结构，用于高效地处理数组的前缀和问题，尤其在大规模数据集下具有显著优势。在解题过程中，当我们需要维护一个数组A的前缀和S[i]，即S[i] = A[1] + A[2] + ... + A[i]时，如果频繁修改A[i]，传统的做法会导致前缀和数组S[]的更新时间复杂度为O(n)。然而，树状数组通过将数组划分成若干大小为2的幂次级的子树，每个子树的和存储在一个单独的数组C[]中，解决了这个问题。 树状数组的关键概念包括： 1. **数组C的定义**：C[i]表示A[i-2^k+1]到A[i]的和，其中k是i的二进制表示中末尾0的个数，即i的最小2的幂次。C数组的长度通常是2的某个幂，以支持快速的查找和更新操作。 2. **树的高度**：树状数组的树高不超过logn，因为每个节点的索引k决定了子树的规模，而子树大小是2的幂，这意味着树的高度可以通过计算log2(n)来确定。 3. **修改操作**：当我们需要更新A[i]时，只需改变C[i]及与其相关的C数组元素，由于树的高度限制，这个过程的时间复杂度是O(logn)。可以通过公式p = i + i&(i^(i-1))找到父节点的索引，这里的&操作用于找到最低有效位。 4. **求和操作**：求前n项和只需要找到所有小于n的2的幂，它们对应于树中的子树，然后将这些子树的根节点C值相加。子树的数量由n在二进制表示中1的个数决定，这也保证了求和操作的时间复杂度为O(logn)。 5. **辅助函数**：代码中提供了两个实用函数，`intLowbit(int t)`用于求最小的2的幂次，即t的最低有效位，这对于计算父节点索引很有帮助；求前n项和的操作则依赖于找到适当的子树范围。 理解并掌握树状数组的原理和算法，可以帮助我们在解决需要频繁进行前缀和计算或区间更新的问题时，提高代码的执行效率，特别适用于大规模数据集的应用场景。通过实际的代码实现，可以进一步加深对树状数组构造和操作的理解。