The Scientist and Engineer's Guide to Digital Signal Processing40
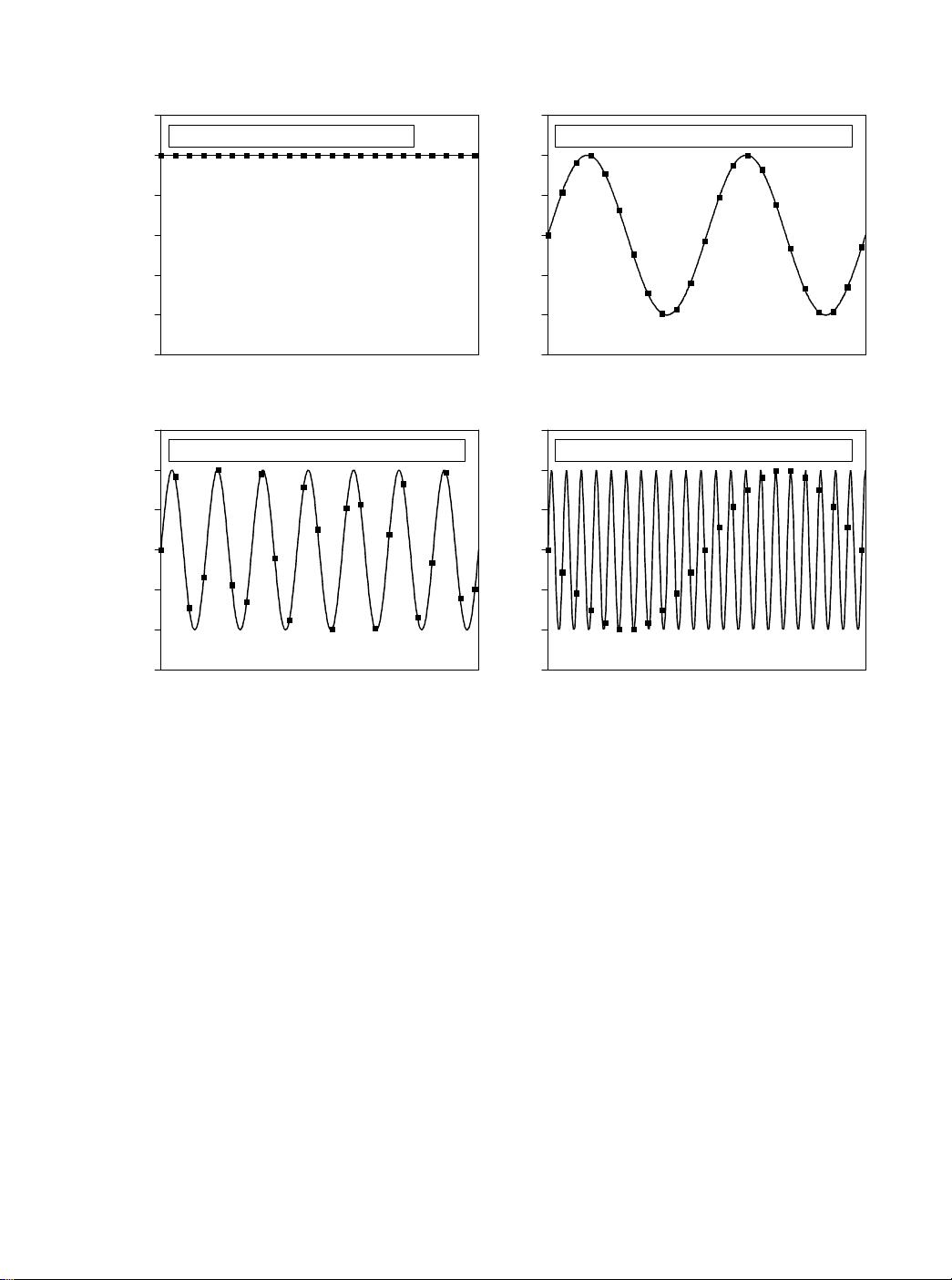
The sine wave shown in (b) has a frequency of 0.09 of the sampling rate. This
might represent, for example, a 90 cycle/second sine wave being sampled at
1000 samples/second. Expressed in another way, there are 11.1 samples taken
over each complete cycle of the sinusoid. This situation is more complicated
than the previous case, because the analog signal cannot be reconstructed by
simply drawing straight lines between the data points. Do these samples
properly represent the analog signal? The answer is yes, because no other
sinusoid, or combination of sinusoids, will produce this pattern of samples
(within the reasonable constraints listed below). These samples correspond to
only one analog signal, and therefore the analog signal can be exactly
reconstructed. Again, an instance of proper sampling.
In (c), the situation is made more difficult by increasing the sine wave's
frequency to 0.31 of the sampling rate. This results in only 3.2 samples per
sine wave cycle. Here the samples are so sparse that they don't even appear
to follow the general trend of the analog signal. Do these samples properly
represent the analog waveform? Again, the answer is yes, and for exactly the
same reason. The samples are a unique representation of the analog signal.
All of the information needed to reconstruct the continuous waveform is
contained in the digital data. How you go about doing this will be discussed
later in this chapter. Obviously, it must be more sophisticated than just
drawing straight lines between the data points. As strange as it seems, this is
proper sampling according to our definition.
In (d), the analog frequency is pushed even higher to 0.95 of the sampling rate,
with a mere 1.05 samples per sine wave cycle. Do these samples properly
represent the data? No, they don't! The samples represent a different sine wave
from the one contained in the analog signal. In particular, the original sine
wave of 0.95 frequency misrepresents itself as a sine wave of 0.05 frequency
in the digital signal. This phenomenon of sinusoids changing frequency during
sampling is called aliasing. Just as a criminal might take on an assumed name
or identity (an alias), the sinusoid assumes another frequency that is not its
own. Since the digital data is no longer uniquely related to a particular analog
signal, an unambiguous reconstruction is impossible. There is nothing in the
sampled data to suggest that the original analog signal had a frequency of 0.95
rather than 0.05. The sine wave has hidden its true identity completely; the
perfect crime has been committed! According to our definition, this is an
example of improper sampling.
This line of reasoning leads to a milestone in DSP, the sampling theorem.
Frequently this is called the Shannon sampling theorem, or the Nyquist
sampling theorem, after the authors of 1940s papers on the topic. The sampling
theorem indicates that a continuous signal can be properly sampled, only if it
does not contain frequency components above one-half of the sampling rate.
For instance, a sampling rate of 2,000 samples/second requires the analog
signal to be composed of frequencies below 1000 cycles/second. If frequencies
above this limit are present in the signal, they will be aliased to frequencies
between 0 and 1000 cycles/second, combining with whatever information that
was legitimately there.