Matlab实现逻辑回归和线性回归算法详解

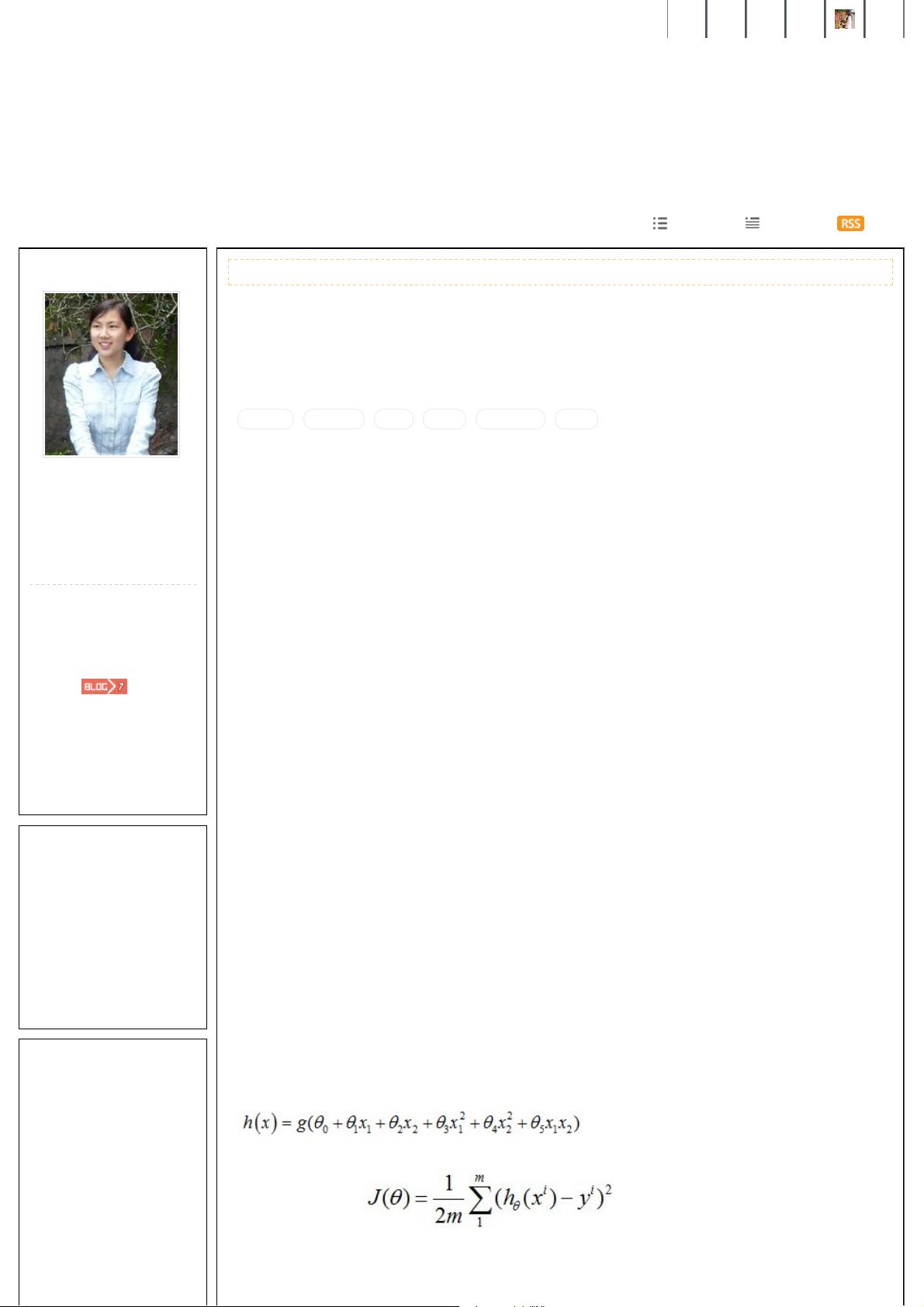
Matlab实现逻辑回归 Matlab是流行的计算工具之一，广泛应用于科学计算、数据分析、机器学习等领域。本文将详细介绍如何使用Matlab实现逻辑回归，并对逻辑回归的基本模型、梯度下降算法、cost function等进行详细的解释。 一、逻辑回归的基本模型 逻辑回归是一种常用的机器学习算法，用于解决二分类问题。其基本模型可以表述为： Y = 1 / (1 + e^(-z)) 其中，z是输入参数，Y是输出结果。逻辑回归的基本模型可以用sigmoid函数来描述。 二、梯度下降算法 梯度下降算法是逻辑回归中常用的优化算法。其主要思想是：通过不断迭代来找到使cost function最小的参数值。cost function可以表述为： J(θ) = (1/2) * ∑(y - h(x))^2 其中，θ是参数，y是真实值，h(x)是预测值。梯度下降算法的主要步骤为： 1. 初始化参数θ 2. 计算cost function J(θ) 3. 计算梯度gradient 4. 更新参数θ 5. 重复步骤2-4，直到达到最大迭代次数或cost function不再减小 三、Matlab实现逻辑回归 使用Matlab实现逻辑回归可以通过以下步骤： 1. 定义cost function 2. 实现梯度下降算法 3. 使用Matlab的plot函数可视化结果 以下是Matlab代码的示例： ``` function [jVal, gradient] = costFunction(theta) % 计算cost function jVal = (1/2) * sum((y - h(x))^2); % 计算梯度 gradient = -(y - h(x)) * x; end function [optTheta, functionVal, exitFlag] = Gradient_descent() % 初始化参数 theta = zeros(n, 1); % 设置迭代次数 maxIter = 1000; % 迭代 for i = 1:maxIter % 计算cost function [jVal, gradient] = costFunction(theta); % 更新参数 theta = theta - alpha * gradient; end end ``` 四、结论 本文详细介绍了Matlab实现逻辑回归的步骤，包括逻辑回归的基本模型、梯度下降算法和Matlab实现的示例代码。通过本文的学习，读者可以更好地理解逻辑回归的原理和实现方式，并应用于实际问题中。