Integer-to-Integer变换下的熵编码优化：降低存储需求的新型变换编码

需积分: 9 39 浏览量更新于2024-09-23 收藏 212KB PDF 举报

"《基于整数到整数变换的变换编码》（Transform Coding with Integer-to-Integer Transforms）是一篇发表在2000年3月《IEEE Transactions on Information Theory》第46卷第2期的研究论文，作者是Vivek K Goyal，他作为IEEE成员提出了一个对变换编码的新理解。这篇论文探讨了一种不同于传统方法的编码策略，它将焦点放在了熵编码而非量化上。在传统的变换编码中，首先计算Karhunen-Loève变换系数，然后进行量化，这使得向量熵编码可以被替换为更简单的标量熵编码，而不会增加编码速率。这种转变的核心优势在于减少了熵编码所需的内存。论文提出了一种新颖的技术，即先对信号样本进行标量量化，然后使用一个整数到整数的非正交线性变换近似。这种方法的独特之处在于，它可能通过使用单一的通用标量熵码本，进一步降低内存需求，特别是对于高比特率编码的高斯源。整数到整数变换编码技术的优点在于它能够在保持编码效率的同时，简化编码过程，这对于处理大量数据的系统来说具有实际意义。然而，与传统的Karhunen-Loève变换相比，这种方法的性能优化可能会受到变换性质、量化策略以及熵编码算法选择的影响。论文还进行了深入的分析，展示了在高比特率编码情况下，这种技术如何有效地减少内存需求，从而提高整体系统的效率和性能。这篇论文不仅提供了一种新的编码框架，还为优化数字信号处理中的内存消耗和编码效率提供了一个新的思考方向，对于理解和改进现代视频编码标准如H.264中的变换编码技术具有重要的理论价值和实践指导意义。"

IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 2, MARCH 2000 465

Transform Coding with Integer-to-Integer Transforms

Vivek K Goyal, Member, IEEE

Abstract—A new interpretation of transform coding is de-

veloped that downplays quantization and emphasizes entropy

coding, allowing a comparison of entropy coding methods with

different memory requirements. With conventional transform

coding, based on computing Karhunen–Loève transform coef-

ficients and then quantizing them, vector entropy coding can

be replaced by scalar entropy coding without an increase in

rate. Thus the transform coding advantage is a reduction in

memory requirements for entropy coding. This paper develops

a transform coding technique where the source samples are first

scalar-quantized and then transformed with an integer-to-integer

approximation to a nonorthogonal linear transform. Among the

possible advantages is to reduce the memory requirement further

than conventional transform coding by using a single common

scalar entropy codebook for all components. The analysis shows

that for high-rate coding of a Gaussian source, this reduction

in memory requirements comes without any degradation of

rate-distortion performance.

Index Terms—Entropy coding, Gaussian sources, memory re-

duction, transform coding.

I. INTRODUCTION

RANSFORM coding is the most successful and perva-

sive technique for lossy compression of audio, images,

and video. The conventional framework of transform coding

was introduced by Huang and Schultheiss [1]

: one is given a

discrete-time, continuous-valued, vector source with correlated

components; instead of quantizing the components separately,

one uses a linear transform to compute transform coefficients

and scalar-quantizes the transform coefficients. In either case,

entropy codes may be used to improve the coding efficiency.

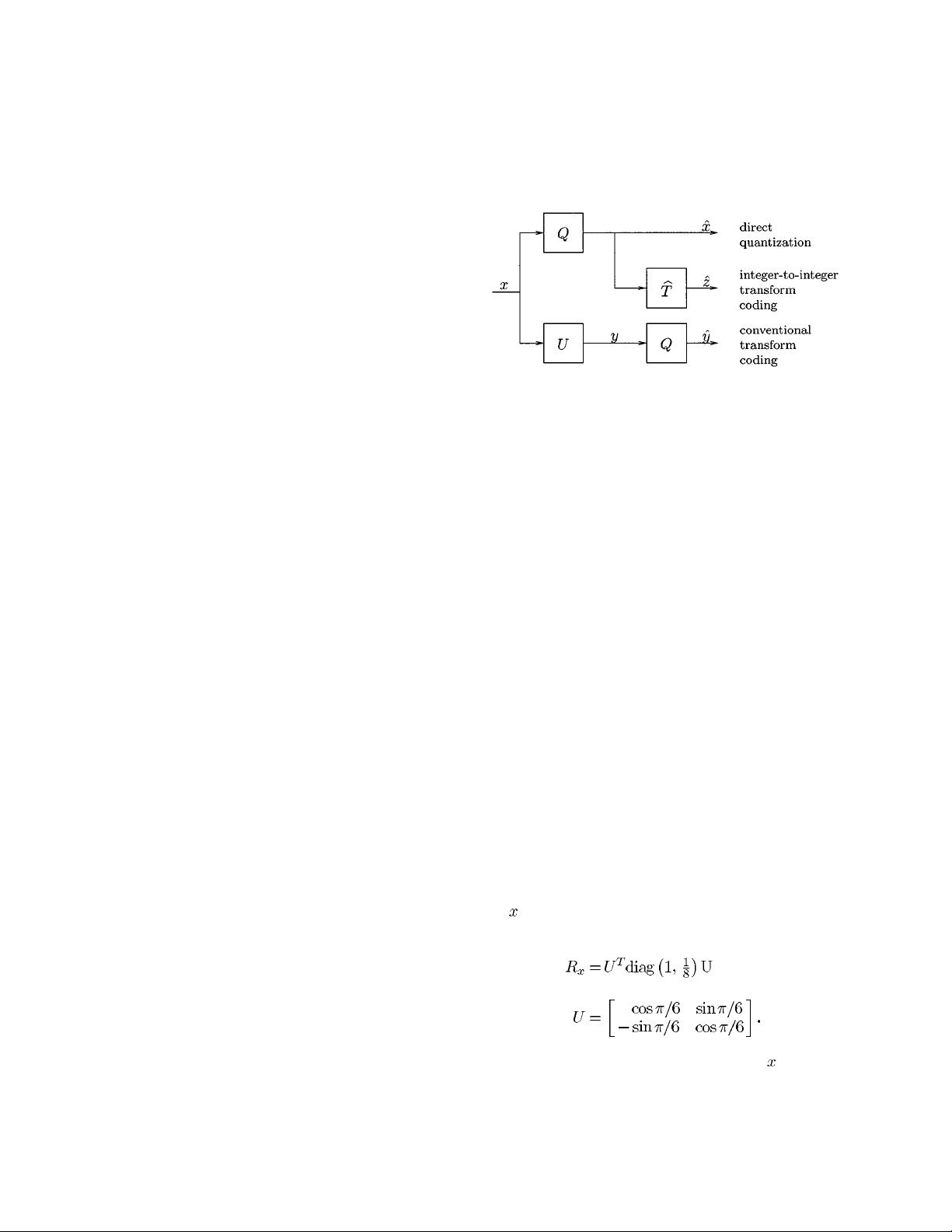
Transform coding is contrasted to direct quantization in the top

and bottom paths of Fig. 1.

Transform coding is an inherently suboptimal source coding

technique because it uses the Cartesian product of scalar

quantizers, called simply a scalar quantizer. Compared to an

appropriately designed vector quantizer, a scalar quantizer has

a space-filling loss [3], [4] that cannot be neutralized by linear

pre- and post-processing. This is caused by the high second

moment of a cube, as compared to a sphere of the same volume.

On the other hand, transform coding has much lower com-

plexity than less constrained forms of vector quantization. Thus

transform coding is often called a low-complexity alternative

Manuscript received March 16, 1999; revised September 24, 1999. The ma-

terial in this paper was presented in part at the 32nd Asilomar Conference on

Signals, Systems, and Computers, Pacific Grove, CA, November 1–4, 1998.

The author is with the Mathematics of Communications Research Depart-

ment, Bell Laboratories, Lucent Technologies, Murray Hill, NJ 07974-0636

USA.

Communicated by P. A. Chou, Associate Editor for Source Coding.

Publisher Item Identifier S 0018-9448(00)01363-8.

Earlier work by Kramer and Matthews [2] did not include quantization;

hence, it is disconnected from the current practice of transform coding.

Fig. 1. Schematic representation of a system that produces the three

representations considered in this paper.

to vector quantization. The transform changes coordinates to

improve the performance of scalar quantization.

The discussion above places great emphasis on quantization.

This paper shows that this emphasis is undue. At high rates,

the performance obtained by Huang and Schultheiss can be

matched by a system that quantizes the original source compo-

nents and then uses a transform to reduce scalar entropy (see the

middle path of Fig. 1). This suggests that the value of transform

coding comes not from changing the coordinate system for

quantization, but almost exclusively from decorrelation.

The most important feature of the proposed system is that

the transform is now discrete, not continuous as before. It is

shown that the transform can be designed so that the memory

requirement of the entropy coding block is reduced without sac-

rificing rate-distortion performance. Also, since the source is

immediately discretized, it is not important that it is contin-

uous-valued. Thus the techniques described here can be applied

to discrete-valued sources.

The paper is organizedasfollows: Section II gives an example

of the proposed scheme to provide motivation for the general

framework, which is described in Section III. Section IV sum-

marizes the results.

II. A

N ILLUSTRATIVE EXAMPLE

Let be a Gaussian random vector with mean zero and co-

variance matrix

where

We will compare three methods for representing with approx-

imately the same mean-squared error (MSE) distortion. These

methods all include uniform scalar quantization; they differ in

their use of transforms, as shown in Fig. 1. Each of the three is

then combined with different forms of entropy coding, yielding

下载后可阅读完整内容，剩余8页未读，立即下载

adamshi_126

粉丝: 2
资源: 16

Integer-to-Integer变换下的熵编码优化：降低存储需求的新型变换编码

高效备战技术面试：leetcode苹果-coding-interview-prep-today

"小林coding：图解系统-亮白风格-v1.0.pdf

SAP顾问必备资源：全英文档清单

Coding-Projects-in-Python.pdf.pdf

IEEE.Standard.Codecs.Image.Compression.To.Advanced.Video.Coding.eBook-LiB.chm

The-Ultimate-Strategy-to-Preparing-for-a-Coding-Interview-Medium.pdf

El-Gamal-A.--Kim-Y.-H.-Network-Information-Theory_Coding Theory_

Cracking-the-Coding-Interview-Dragged.pdf

sei-cert-c-coding-standard-2016-v01.pdf

sei-cert-cpp-coding-standard-2016-v01.pdf

最新资源