BP神经网络优化方法与Matlab实例：预测公路运力

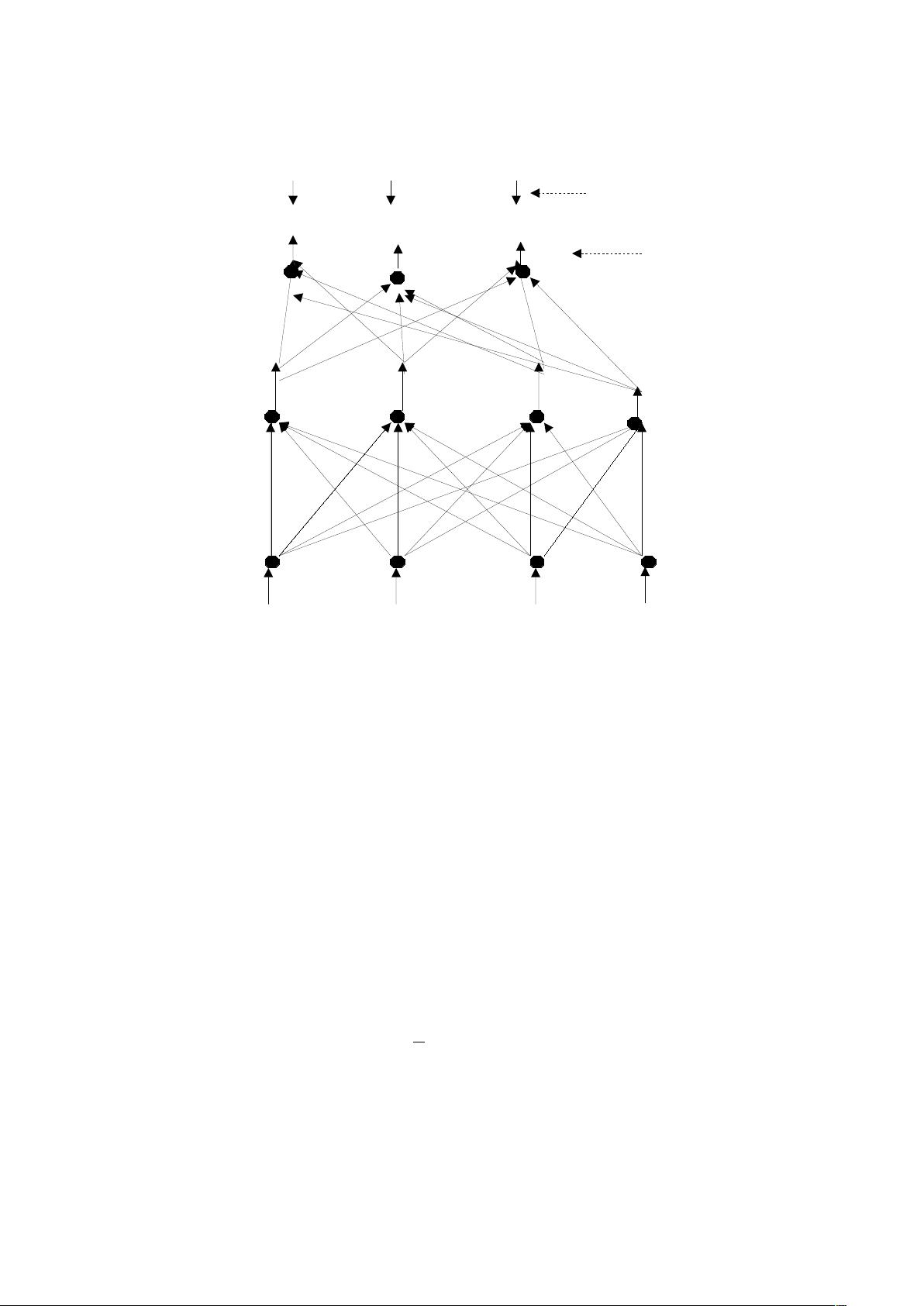
BP神经网络算法是一种用于解决非线性问题的常用机器学习技术，尤其适用于模式识别、预测和函数逼近等领域。本文主要介绍了三层BP神经网络的基本结构和优化方法，包括反向传播（Backpropagation）的调整策略。 首先，BP神经网络由输入层、一个或多个隐藏层以及输出层组成。输入层接收原始数据，隐藏层通过激活函数进行非线性变换，而输出层则根据特定的传递函数计算结果。对于三层网络，设输入为x，隐含层有h个神经元，其输出记为h，输出层有m个神经元，输出为y，目标输出为y_target。 隐藏层和输出层的传递函数分别为f和g，误差E是网络输出y与目标输出y_target之间的差异，是网络学习的目标。为了最小化误差，BP算法采用梯度下降法，沿着误差函数的负梯度方向更新权值。学习速率α是决定每次更新幅度的重要参数。 在BP神经网络的调整过程中，遵循以下步骤： 1. 隐含层到输出层的权值更新： - 计算输出层神经元的输入z_k，然后使用链式法则（复合函数偏导公式）求得偏导数，得到权重调整公式 Δwjk = -α * δ_k * x_j，其中δ_k是输出层误差关于隐含层的局部误差项。 2. 输入层到隐含层的权值更新： - 对于每个隐藏层神经元，它与所有输出层神经元相连，因此需要考虑所有权重的更新。输入层到隐含层的权重更新公式为 Δwij = -α * δ_j * x_i，这里δ_j是隐含层误差关于输入层的局部误差项，它涉及到与所有输出层神经元的交互。 以实际案例为例，该算法被用于公路运力预测模型的构建。通过给定的历史数据，如公路客运量、机动车数和公路面积，训练BP神经网络以预测2010年和2011年的数据。在MATLAB中，通过定义函数并设置适当的参数（如输入维度、输出维度、隐藏层神经元数量等），可以实现数据预处理、网络训练和预测功能。 总结来说，BP神经网络算法利用反向传播原理来优化网络结构，通过调整权重来减小误差，进而提高预测准确性。这种算法在处理复杂的输入-输出映射关系时表现出强大的适应性，是现代机器学习中不可或缺的一部分。