Assume that the value of the segment point is being sought for a sample in the range between x
1
and x
2
. An entropy equa-
tion is written for the regions ½x
1
; x and ½x; x
2
, and denotes the first region p and the second region q. Entropy with each value
of x is expressed as: [14]
SðxÞ¼pðxÞS
p
ðxÞþqðxÞS
q
ðxÞ ð7Þ
where
S
p
ðxÞ¼½p
1
ðxÞln p
1
ðxÞþp
2
ðxÞln p
2
ðxÞ
S
q
ðxÞ¼½q
1
ðxÞln q
1
ðxÞþq
2
ðxÞln q
2
ðxÞ
ð8Þ
and where p
k
ðxÞ and q
k
ðxÞ are the conditional probabilities that the class k sample is in region ½x
1
; x
1
þ x and ½x
1
þ x; x
2
,
respectively, and pðxÞ and q(x) are the probabilities that all samples are in region ½x
1
; x
1
þ x and ½x
1
þ x; x
2
, respectively.
pðxÞþqðxÞ¼1 ð9Þ
The value of x that gives the minimum entropy is the optimum value of the segment point. The entropy estimates of pk(x)
and qk(x), and p(x) and q(x) are calculated, as follows: [14]
pkðxÞ¼
n
k
ðxÞþ1
nðxÞþ1
ð10Þ
qkðxÞ¼
N
k
ðxÞþ1
NðxÞþ1
ð11Þ
pðxÞ¼
nðxÞ
n
ð12Þ
qðxÞ¼1 pðxÞ ð13Þ
where nk(x) is the number of class k samples located in ½x1; x1 þ x, n(x) is the total number of samples located in ½x1; x1 þ x,
Nk(x) is the number of class k samples located in ½x1 þ x; x2, N(x) is the total number of samples located in ½x1 þ x; x2, and n
is the total number of samples in [x1, x2].
2.4. Rough set theory
Rough sets theory (RST) was proposed by Pawlak [33–37] in 1982. In recent years, RST has been used in economic and
financial prediction. Many researchers have applied RST to discover trading rules [20,48]. The concept of RST is founded
on the assumption that with every associated object of the universe of discourse, some information objects characterized
by the same information are indiscernible in the view of the available information about them. Any set of all indiscernible
objects is called an elementary set and forms a basic granule of knowledge about the universe. Any union of elementary sets
is referred to as a precise set; otherwise the set is rough.
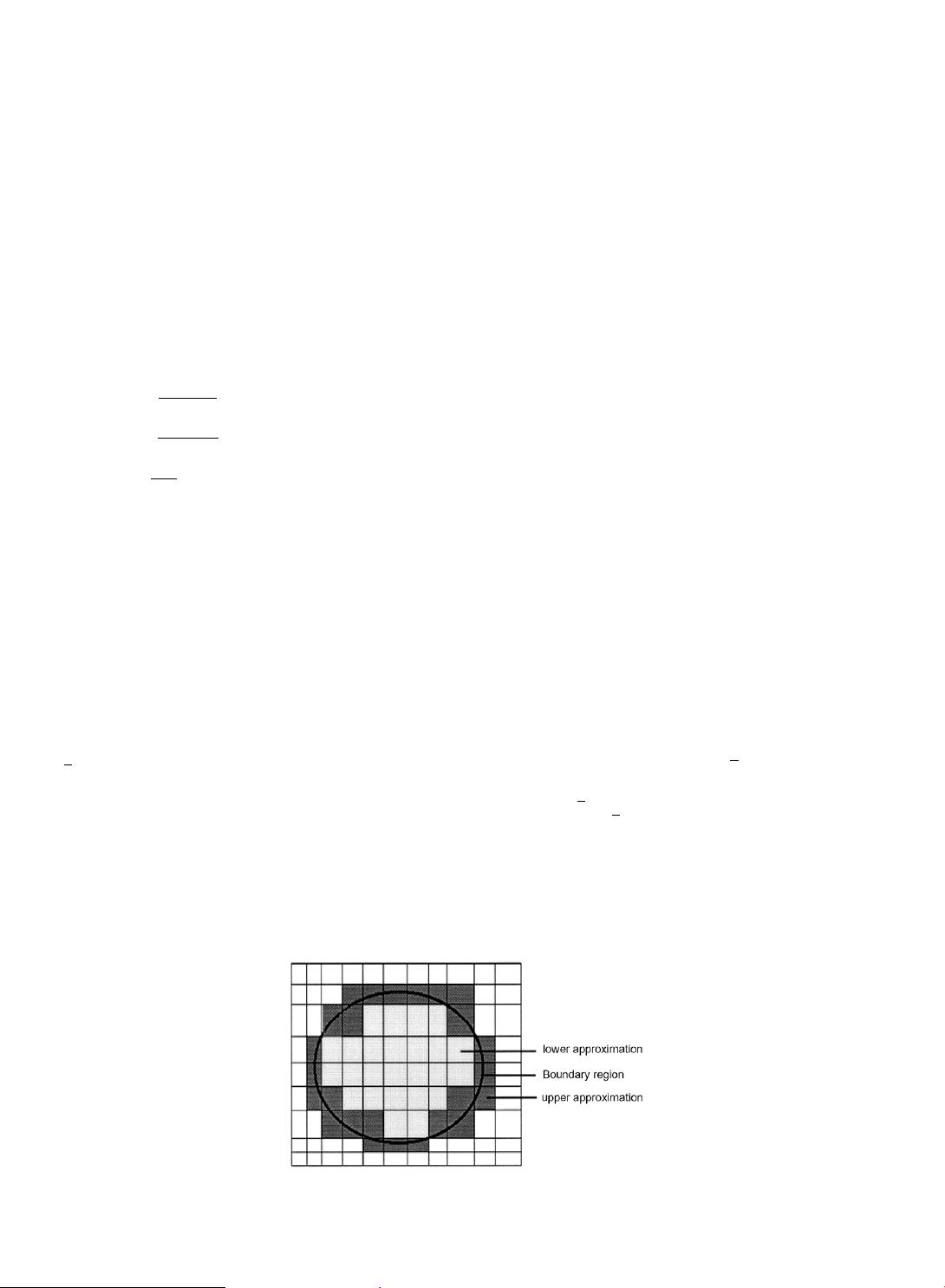
With any rough sets, a pair of precise sets, called the lower and upper approximation,
BX ¼fxj½x
B
# Xg and
BX ¼fxj½x
B
\ X – ;g of the rough sets, is associated [33]. The lower approximation consists of all objects that definitely be-
long to the set, and the upper approximation contains all objects that possibly belong to the set. The difference between the
upper and the lower approximation constitutes the boundary region, BN
B
ðxÞ¼BX BX, of the rough sets. The set X is called
‘‘rough” (or ‘‘roughly definable”) with respect to the knowledge in B, if the boundary region is non-empty. The basic notions
in rough sets are shown in Fig. 1.
The RST is a series of logical reasoning procedures used for analyzing an information system. An information system can
be seen as a decision table, denoted by S ¼ðU; A; C; DÞ, where U is the universe of discourse, A is a set of primitive features,
and C; D A are two subsets of features, assuming that A ¼ C [D and C \ D ¼;, where C is called the condition attribute and
D is the decision attribute. The measure to describe the inexactness of approximation classifications is called the quality of
Fig. 1. Basic notions of rough sets.
C.-H. Cheng et al. / Information Sciences 180 (2010) 1610–1629
1613









