统计过程控制SPC：原理、图表与应用

"统计制程管制SPC.pdf" 统计过程控制（Statistical Process Control, SPC）是一种利用统计方法监控和改善生产过程的方法，旨在确保产品的质量和一致性。它由美国的休哈特博士在1924年提出，通过3Sigma原理应用于生产过程中，通过控制图来识别和控制生产过程中的变异。 SPC的主要目标包括： 1. 持续稳定性：通过SPC，可以确保生产过程处于受控状态，减少不必要的波动，从而维持稳定的产品质量。 2. 提高质量与效率：通过减少不良品率，SPC有助于提高产品的合格率，同时降低返工和废品成本，从而提升整体生产效率。 3. 决策依据：SPC提供的数据可用于分析和改进过程，为管理层决策提供有力支持。 4. 区分变异原因：SPC能区分出变差的特殊原因和普通原因，帮助确定是采取局部改进措施还是对整个系统进行调整。 SPC涉及的关键术语包括： - 平均值(X)：一组测量值的算术平均。 - 极差(Range)：样本中的最大值与最小值之差，反映数据的离散程度。 - σ（Sigma）：标准差的希腊字母表示，衡量数据分布的离散程度。 - 标准差：衡量样本或总体数据点相对于平均值的偏差程度。 - 分布宽度(Spread)：数据分布的范围，从最小值到最大值的距离。 - 中位数(˜x)：数据集的中间值，不受极端值影响，反映数据的集中趋势。 - 单值(Individual)：单个产品或特性的一个测量值。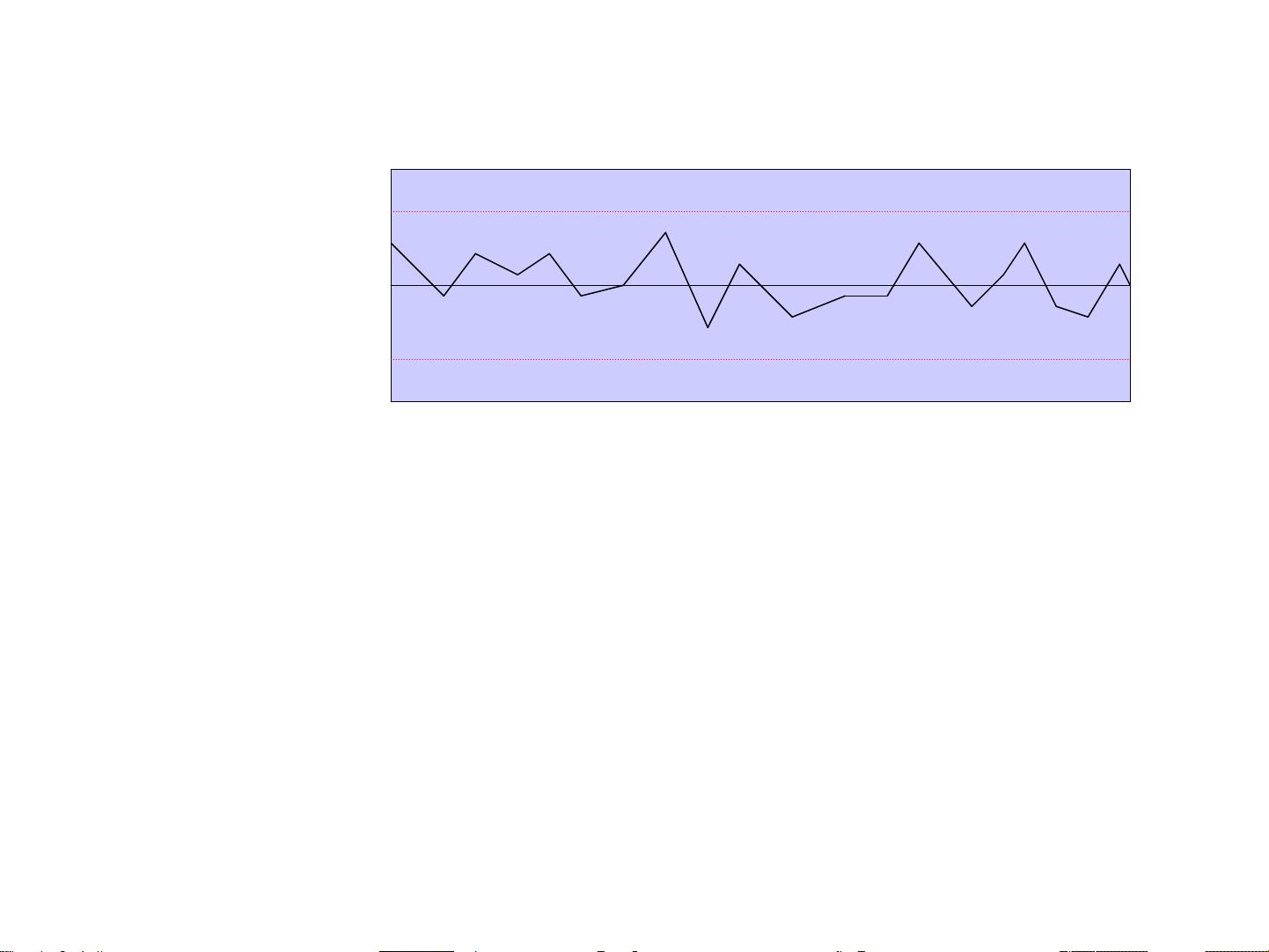 在SPC中，控制图扮演着核心角色，它们包括： - 计量型数据管制图：用于连续或定量数据，如X-R图（单值-极差图）、X-s图（单值-标准差图）、˜X-R图（平均值-极差图）和X-MR图（单值-移动极差图）。 - 计数型数据管制图：适用于二元或计数数据，如p图（不合格品率图）、np图（不合格品数图）、c图（单位缺陷数图）和u图（单位面积缺陷数图）。 选择合适的管制图取决于数据类型和过程特性。正确应用控制图可以帮助监控过程性能，及时发现异常情况，以便采取适当的纠正措施，防止不良品的产生，推动过程持续改进。通过实施SPC，企业能够建立一个反馈机制，不断优化生产流程，达到更高的质量和效率水平。