MATLAB模拟：探索混沌系统的关键特性

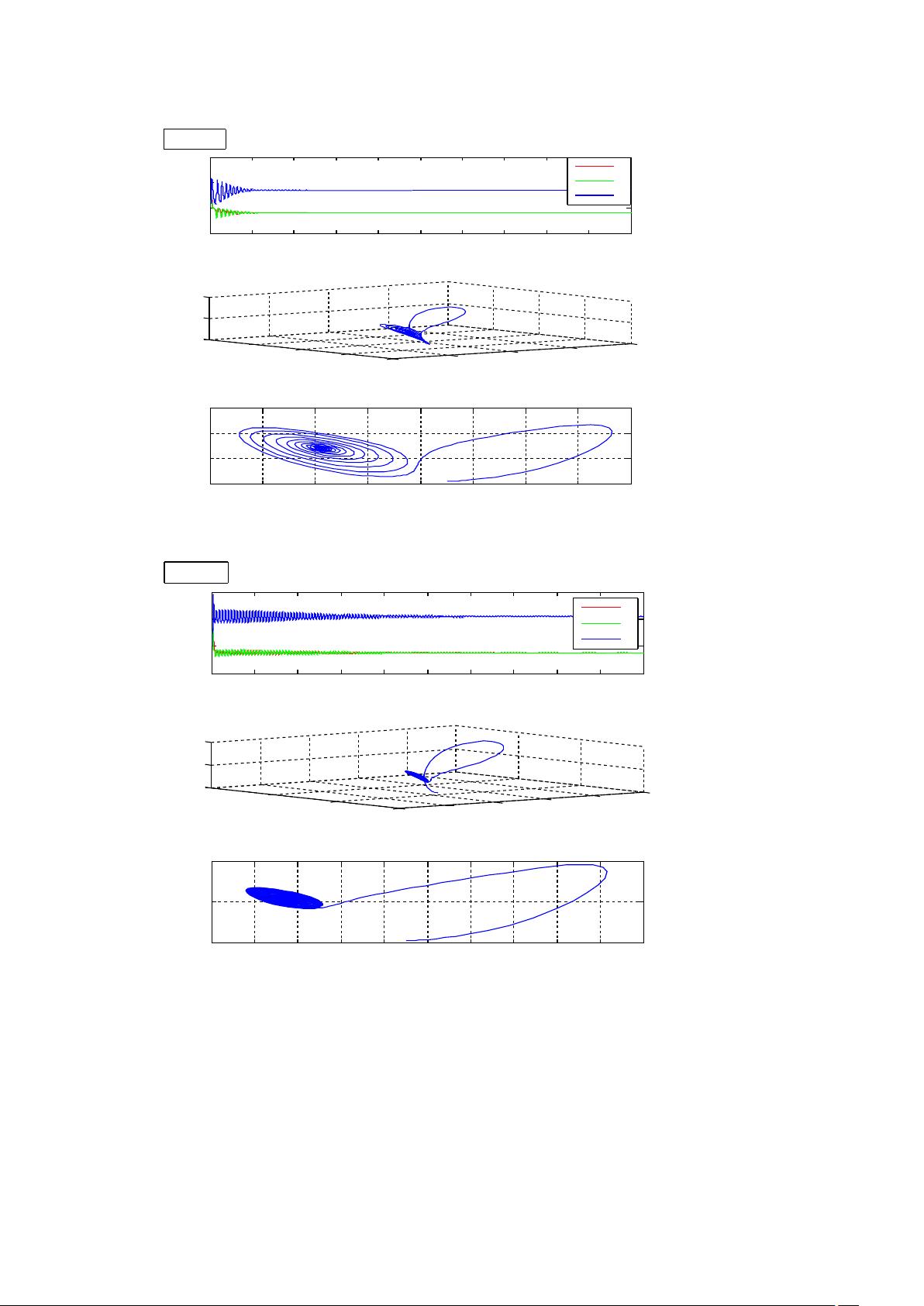
本篇文档详细介绍了如何利用MATLAB这一强大的数学软件来模拟和研究各类混沌系统，它是《混沌实验教学平台的设计与实现》一书中的初期报告。MATLAB在此过程中被用来计算诸如Lorenz系统在内的六个关键混沌模型，这些模型展示了一系列混沌现象，如混沌吸引子、倍周期性、初值敏感性以及相图和分岔图。通过这些数值计算，学习者能够深入理解混沌的复杂性，包括它的非线性本质和不可预测性。 混沌理论起源于1972年E.N.洛伦兹的著名论文《蝴蝶效应》，他揭示了即使是微小的初始条件变化也可能导致长期行为的巨大差异，这是由系统内在的混沌性导致的。混沌运动并非随机，而是确定性系统中的高度不稳定行为，相邻轨迹在时间推移下会呈现出指数级分离，表现出看似随机的运动规律。 相空间在混沌系统的研究中扮演重要角色，它是由一阶微分方程描述的动态系统状态的可视化工具，每个状态对应相空间中的一个点，积分曲线的唯一性反映了系统的演化路径。混沌运动正是在这种相空间中展现其独特的复杂性。 分形和分维的概念也被用于描述混沌系统的几何结构，它们展示了混沌点集在不同尺度下的自相似性和多尺度的复杂性。这种无限精细的结构使得混沌系统在直观上显得无序，但实际上隐藏着深层次的规律。 本文提供了一种教学方法，通过MATLAB的实践操作，帮助读者掌握混沌系统的基本概念和行为特征，这对于理解自然界的复杂系统，如天气预测、生态学、物理学等领域具有重要意义。同时，这也是一种培养学生问题解决能力、数学建模技巧和计算机模拟技能的有效途径。