倒立摆控制系统分析：根轨迹与频域方法

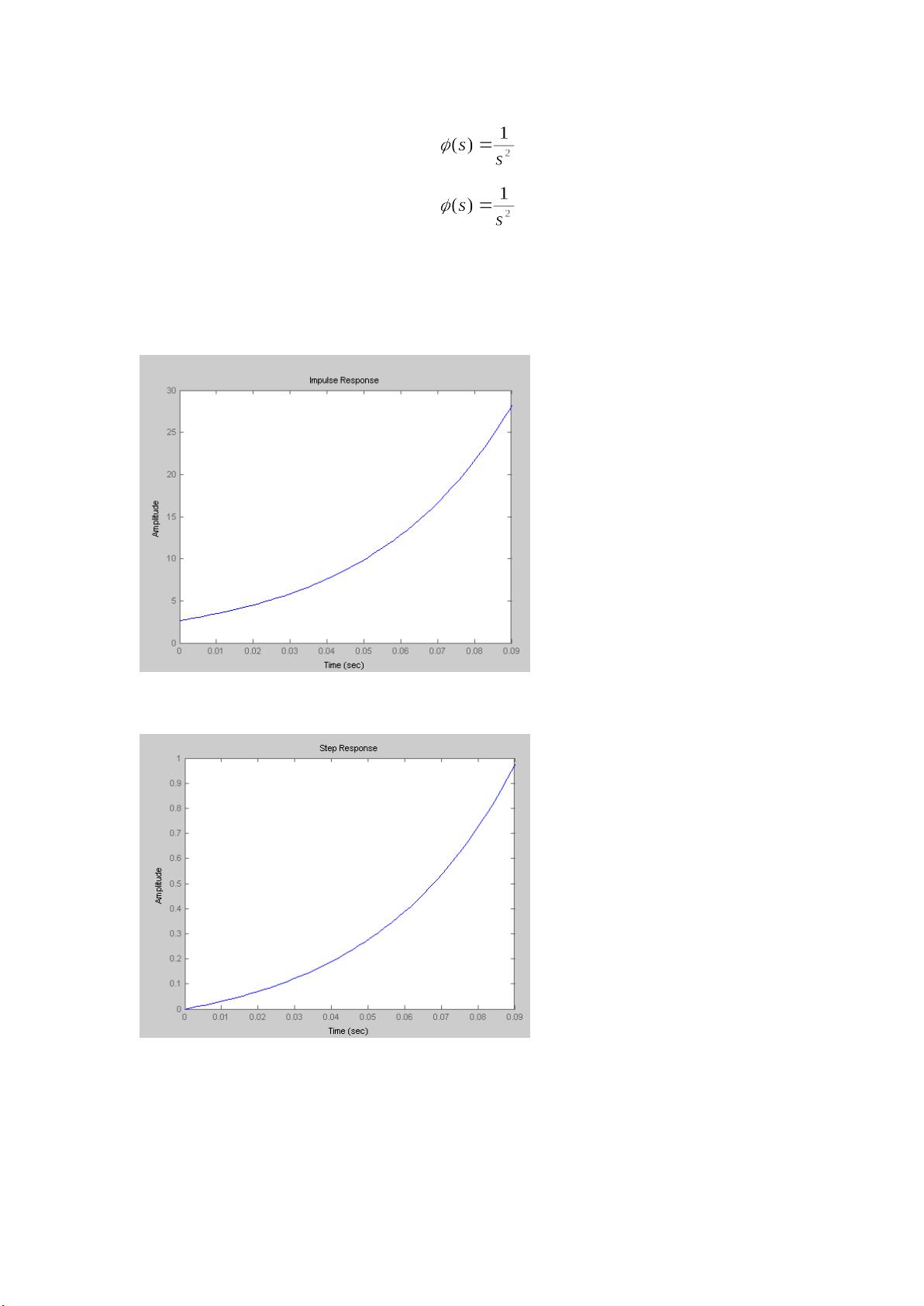
本文主要探讨了倒立摆的校正方法，包括时域校正、频域校正和反馈矫正，以确保系统的稳定性。文章详细介绍了倒立摆的特性和数学模型，特别是针对直线倒立摆进行了深入分析。 1. 倒立摆的基本概念与特点 - 倒立摆是一种特殊的物理系统，其重心位于支撑点之上，处于不稳定状态。 - 非线性：倒立摆系统是非线性的，需要通过线性化处理进行控制设计。 - 不确定性：模型误差、机械间隙和阻力等因素导致不确定性，可通过减少误差来改善。 - 耦合性：各部件间存在强烈的耦合关系，通常在平衡点附近进行解耦计算。 - 开环不稳定性：垂直向上的平衡点是不稳定的，而垂直向下是稳定的。 - 约束限制：如行程和力矩限制，这些因素会影响系统的操作范围。 2. 直线倒立摆数学模型 - 微分方程推导：描述倒立摆动态行为的数学模型通常由微分方程建立。 - 模型参数：实际系统中，需要考虑具体的参数，如质量、长度、摩擦系数等。 - 开环响应分析：分析未控制系统的动态响应，以了解其自然行为。 3. 根轨迹法校正 - 根轨迹分析：利用根轨迹图评估系统稳定性，并找出控制器设计的依据。 - 根轨迹校正：通过改变控制器参数改变根轨迹，优化系统性能。 - MATLAB计算仿真：借助MATLAB工具进行系统模拟，验证校正效果。 4. 频域法设计控制器 - 频率响应表示：分析系统在不同频率下的响应特性。 - 频率响应分析：了解系统的幅值和相位特性，用于控制器设计。 - 仿真：在MATLAB Simulink环境下，模拟系统频率响应和控制效果。 - 频率法重新校正：根据仿真结果调整控制器参数，进一步优化性能。 5. PID控制器设计 - PID控制分析：PID控制器是广泛应用的反馈控制策略，结合比例、积分和微分三个成分。 - 参数设定与仿真：通过合理选择PID参数，实现系统的稳定控制，并通过仿真验证效果。 6. 结论与心得 - 结果分析：总结控制策略的效果，评估系统稳定性。 - 心得体会：分享作者在研究过程中的理解和体验。 该文深入研究了倒立摆的控制问题，通过多种校正方法提高系统的稳定性，并通过仿真验证了设计的有效性。这些方法对于理解和设计倒立摆系统具有重要的指导价值。