弦图与区间图的概念及判定
需积分: 12 122 浏览量
更新于2024-07-20
收藏 948KB PPTX 举报
"本文主要介绍了弦图和区间图的相关概念,包括图的基本概念,如子图、诱导子图、团、极大团、最大团、最小染色、色数、最大独立集、最小团覆盖以及它们之间的关系。弦图是无向图的一个特例,其特征是任意长度大于3的环都至少有一条弦,即连接环中非相邻节点的边。此外,弦图的每一个诱导子图都是弦图,并且不存在同构于Cn(n>3)的子图。单纯点是弦图判定中的一个重要概念,指的是其邻接点集合加上自身构成一个团的顶点。文章还提到了一个实际应用题目,即判断一个无向图是否为弦图的问题。"
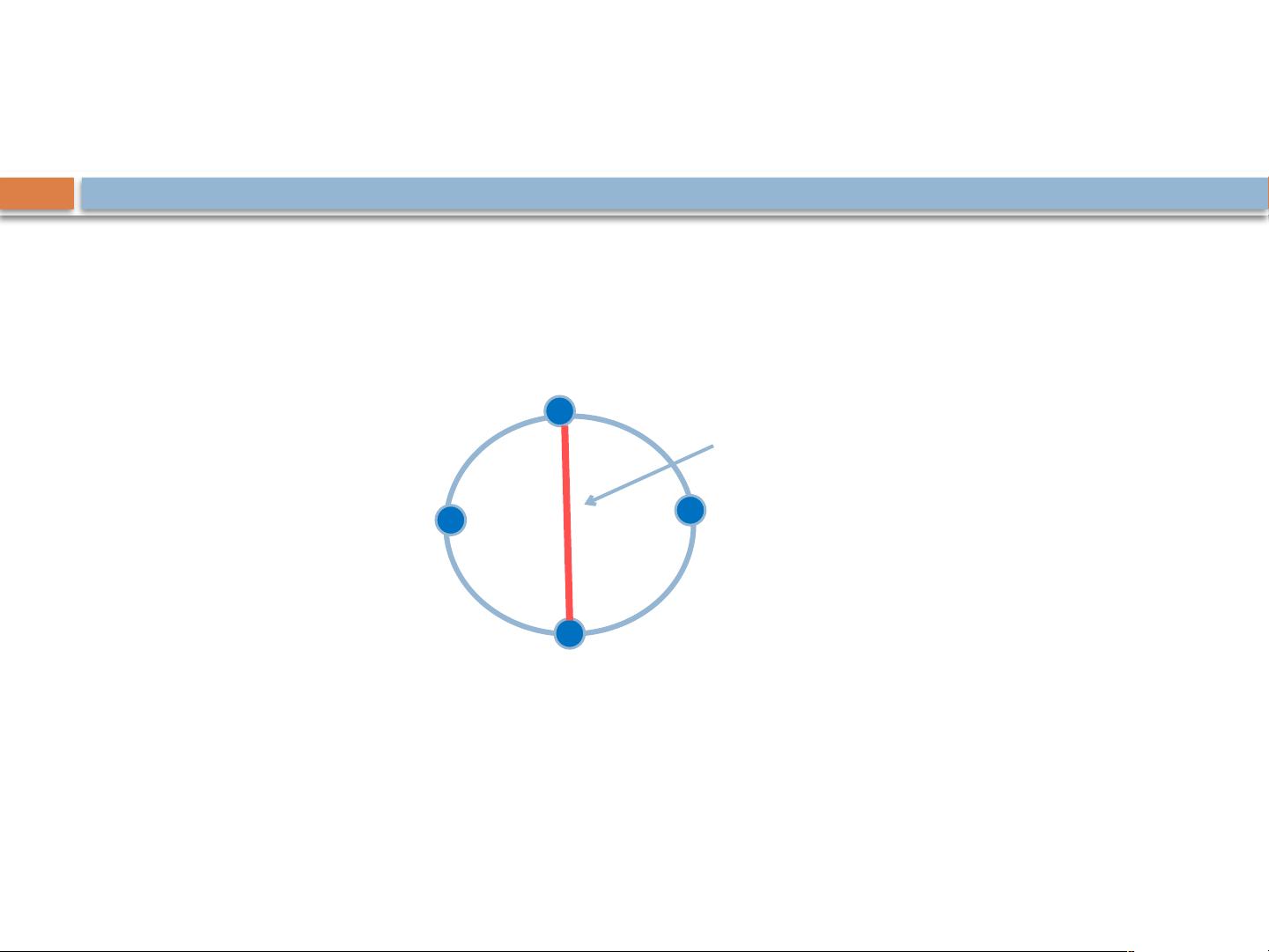
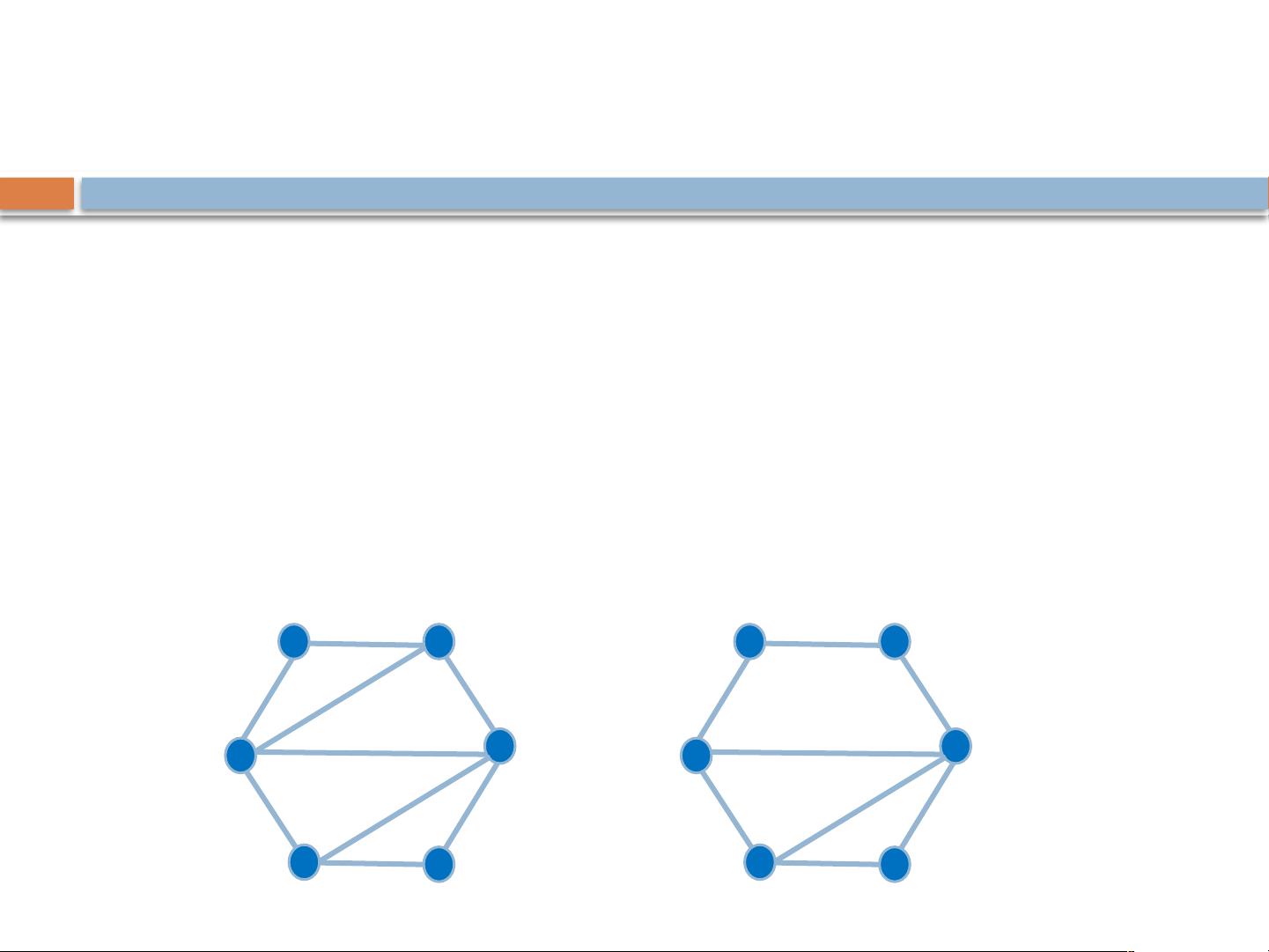
在图论中,弦图是一种特殊的无向图,它的定义基于环的概念。弦图中,如果存在一条边连接了环上不相邻的两个节点,那么这条边被称为弦。弦图的特性是:对于任何长度大于3的环,至少有一个这样的弦存在。这个性质使得弦图没有长度大于3且没有弦的简单环,从而简化了对图结构的分析。
弦图的每一个诱导子图也是弦图,这意味着弦图的任何子集,只要保持原有的边连接关系,仍然是一个弦图。这种性质对于图的分解和算法设计有着重要的意义。同时,弦图不能包含同构于Cn(n>3)的子图,其中Cn代表一个有n个节点的简单环。例如,四边形环C4是可以存在于弦图中的,但五边形环C5则不行,因为它不满足弦的定义。
团是图论中的另一个核心概念,它是指图中的一个子图,该子图内部的每对节点之间都有边相连,形成一个完全图。极大团是指不能再包含更多节点而仍然是团的团,而最大团则是包含节点数最多的团。团数和色数之间有不等式关系,即团数小于等于色数,这来源于图的染色问题。最小染色是指用最少的颜色使图中相邻的节点颜色不同,而色数就是达到这一目标所需的最少颜色数量。
最大独立集是图中最大的一个点子集,其中任意两个点都不相邻。最大独立集数与最小团覆盖数也有不等式关系,最大独立集数不大于最小团覆盖数。最小团覆盖是指用尽可能少的团来覆盖图中的所有节点。
在弦图的判定问题中,单纯点是一个关键的概念。如果一个点v的所有邻居构成的子图是一个团,那么v就是一个单纯点。单纯点的存在可以帮助简化弦图的结构分析,因为它们可以被当作起点逐步构建整个图的团结构。
实际应用中,如题目Zju1015Fishingnet所示,我们需要通过算法来判断给定的无向图是否符合弦图的定义。这个问题可以通过寻找图中的环和弦来解决,也可以利用单纯点的性质进行求解。弦图的判定是图论中的一个重要问题,它不仅有助于理解图的结构,而且在数据结构、算法设计和网络分析等领域有着广泛的应用。
点击了解资源详情
点击了解资源详情
2024-10-18 上传
2021-05-31 上传
2023-02-23 上传
2021-05-22 上传
Leokery
- 粉丝: 29
- 资源: 8
最新资源
- CoreOS部署神器:configdrive_creator脚本详解
- 探索CCR-Studio.github.io: JavaScript的前沿实践平台
- RapidMatter:Web企业架构设计即服务应用平台
- 电影数据整合:ETL过程与数据库加载实现
- R语言文本分析工作坊资源库详细介绍
- QML小程序实现风车旋转动画教程
- Magento小部件字段验证扩展功能实现
- Flutter入门项目:my_stock应用程序开发指南
- React项目引导:快速构建、测试与部署
- 利用物联网智能技术提升设备安全
- 软件工程师校招笔试题-编程面试大学完整学习计划
- Node.js跨平台JavaScript运行时环境介绍
- 使用护照js和Google Outh的身份验证器教程
- PHP基础教程:掌握PHP编程语言
- Wheel:Vim/Neovim高效缓冲区管理与导航插件
- 在英特尔NUC5i5RYK上安装并优化Kodi运行环境