傅立叶变换解析：从理论到FFT

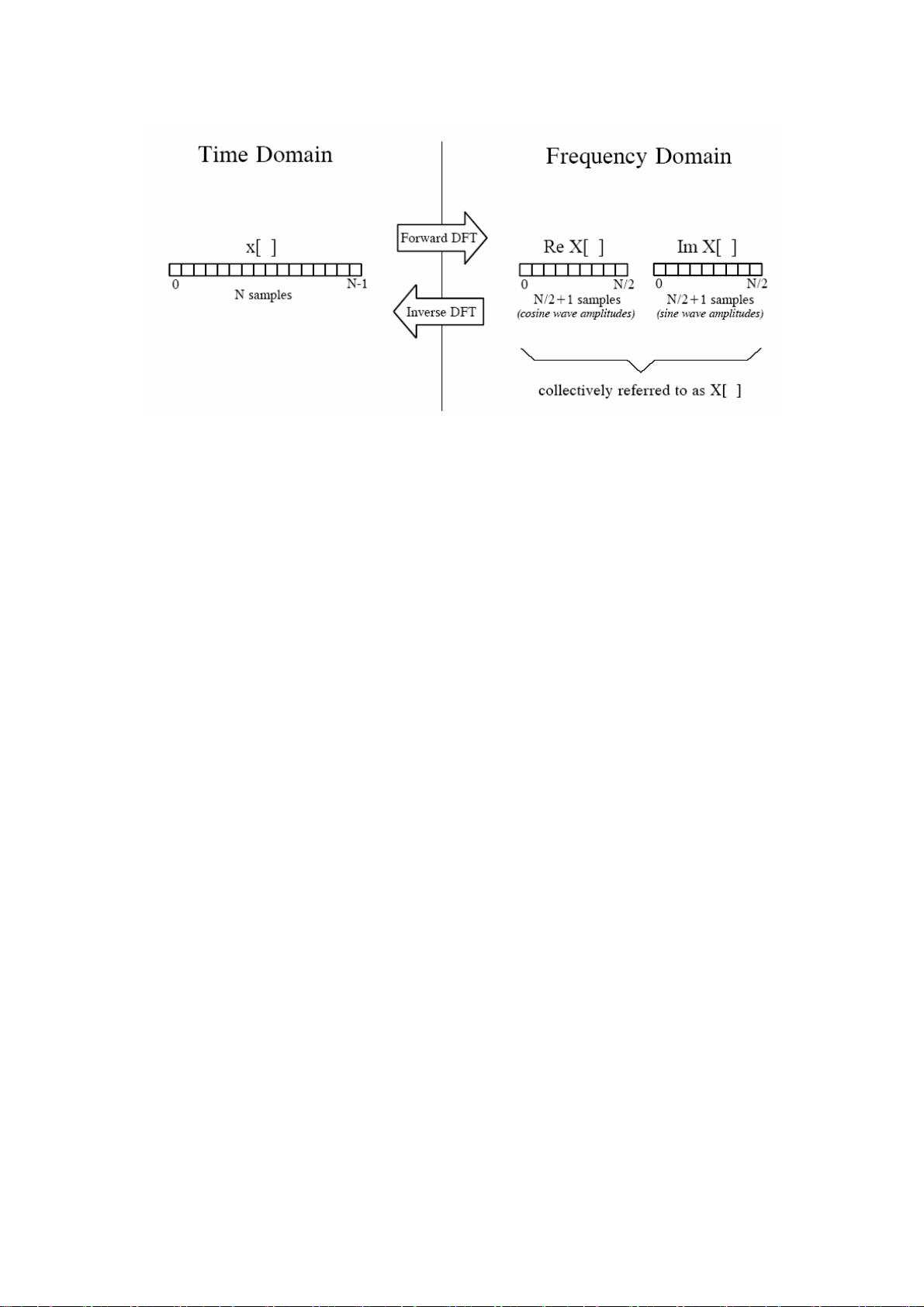
傅立叶变换"来分析和理解这些信号。傅立叶变换是一种数学工具，它将一个时间域或空间域的信号转换为其频域表示，揭示了信号的频率成分。这个概念最初由法国数学家和物理学家傅立叶提出，他在研究热传导问题时发现了这一理论。 傅立叶变换的基本思想是，任何周期性或连续的函数都可以表示为无限多个正弦波的线性组合。这在数学上表现为一个积分公式，将原始函数转换为不同频率的幅度和相位。对于离散信号，我们使用离散傅立叶变换（DFT），它是傅立叶变换在离散时间序列上的应用。 离散傅立叶变换的公式为： \[ X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N} \] 这里，\( x[n] \) 是输入的离散时间序列，\( X[k] \) 是对应的离散频率谱，\( N \) 是序列的长度，\( k \) 是频率索引，\( j \) 是虚数单位。逆离散傅立叶变换（IDFT）则用于将频域表示还原回时域序列： \[ x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j2\pi kn/N} \] FFT，即快速傅立叶变换，是计算离散傅立叶变换的一种高效算法，由Cooley和Tukey在1965年提出。它利用了离散傅立叶变换的对称性和分治策略，将复杂度从O(N^2)降低到O(N log N)。FFT的实现通常包括蝶形运算，通过递归地将序列分为两半进行处理。 在数字信号处理领域，FFT有广泛的应用，例如滤波、频谱分析、信号合成、图像处理等。理解FFT的关键在于掌握其基本原理，包括复数的概念、指数函数的性质以及如何通过复数乘法来实现频率的加减。 对于初学者来说，理解傅立叶变换和FFT可能比较困难，因为涉及到复数运算和傅立叶级数的基础知识。不过，通过逐步学习和实践，可以从简单的例子开始，比如将一个简单的周期性信号分解为正弦波，然后逐渐深入到更复杂的信号分析。此外，阅读像Steven W. Smith博士编写的《数字信号处理指南》这样的资源，可以帮助读者更直观地理解这些概念。 傅立叶变换和FFT是理解和处理周期性或离散信号的重要工具，它们在现代科技，特别是通信、音频处理、图像分析等领域发挥着至关重要的作用。通过深入学习和实践，可以掌握这一强大的数学工具，并将其应用于实际问题中。