基于分解的进化多目标优化算法：MOEA/D综述

需积分: 6 168 浏览量更新于2024-07-16 收藏 1.05MB PDF 举报

"这篇文章是Anupam Trivedi等人发表在IEEE Transactions on Evolutionary Computation期刊上的一篇关于基于分解的进化多目标优化算法（MOEA/D）的综述。文章探讨了分解策略在传统多目标优化中的应用，并特别关注了Zhang和Li于2007年提出的基于分解的多目标进化算法对这一领域的贡献。该算法将多目标优化问题分解为多个标量优化子问题，以此来解决复杂的优化任务。" 在多目标优化领域，进化算法已经成为一种强大的工具，能够处理具有多个相互冲突的目标函数的问题。传统的单目标优化方法往往难以有效地平衡这些目标之间的冲突。基于分解的多目标进化算法（MOEA/D）引入了一种新的策略，它借鉴了分解的思想，将一个复杂的多目标优化问题转化为一系列的单目标子问题。这种分解方法有助于算法更精细地探索决策空间，同时保持解决方案的多样性，从而在多个目标之间达到更好的平衡。 MOEA/D的基本思想是通过构建一个解的子集，即所谓的“帕累托前沿的分解”，每个子问题对应于这个子集的一个部分。这种方法允许算法独立地优化每个子问题，同时确保整个帕累托前沿的均匀覆盖。在算法的进化过程中，每个个体都与子集中的其他个体进行交互，以更新其适应度值和遗传信息。 Zhang和Li的原始算法提出了一个基于边界映射的分解框架，其中，每个子问题的解空间由一个边界点定义。通过调整这些边界点，算法可以动态地调整子问题的分布，以适应问题的特性。此外，他们还引入了一个邻域操作，以促进解的多样性，防止早熟收敛。 MOEA/D的优势在于其灵活性和可扩展性。它可以轻松地结合不同的单目标优化策略，如遗传算子或适应度函数，以适应各种多目标优化问题。此外，MOEA/D框架也鼓励研究者提出新的改进版本和变体，例如通过改进分解方法、调整邻域操作或者引入新的协同机制来进一步提高性能。然而，尽管MOEA/D已经取得了显著的成就，但仍然存在挑战。例如，如何有效地定义和调整子问题的边界、如何选择和更新邻域结构，以及如何衡量和维持解的多样性，都是当前研究的重点。此外，针对动态多目标优化问题、高维度问题以及带有不确定性的优化问题，MOEA/D的适应性和性能仍有待提升。基于分解的多目标进化算法，特别是Zhang和Li的MOEA/D，为多目标优化提供了一种有力的工具。它不仅促进了多目标优化领域的理论发展，也为实际工程和科学问题的解决提供了实用的解决方案。随着技术的不断进步和新方法的涌现，我们可以期待MOEA/D在未来将继续发挥重要作用，并为多目标优化带来更多的突破。

1089-778X (c) 2016 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TEVC.2016.2608507, IEEE

Transactions on Evolutionary Computation

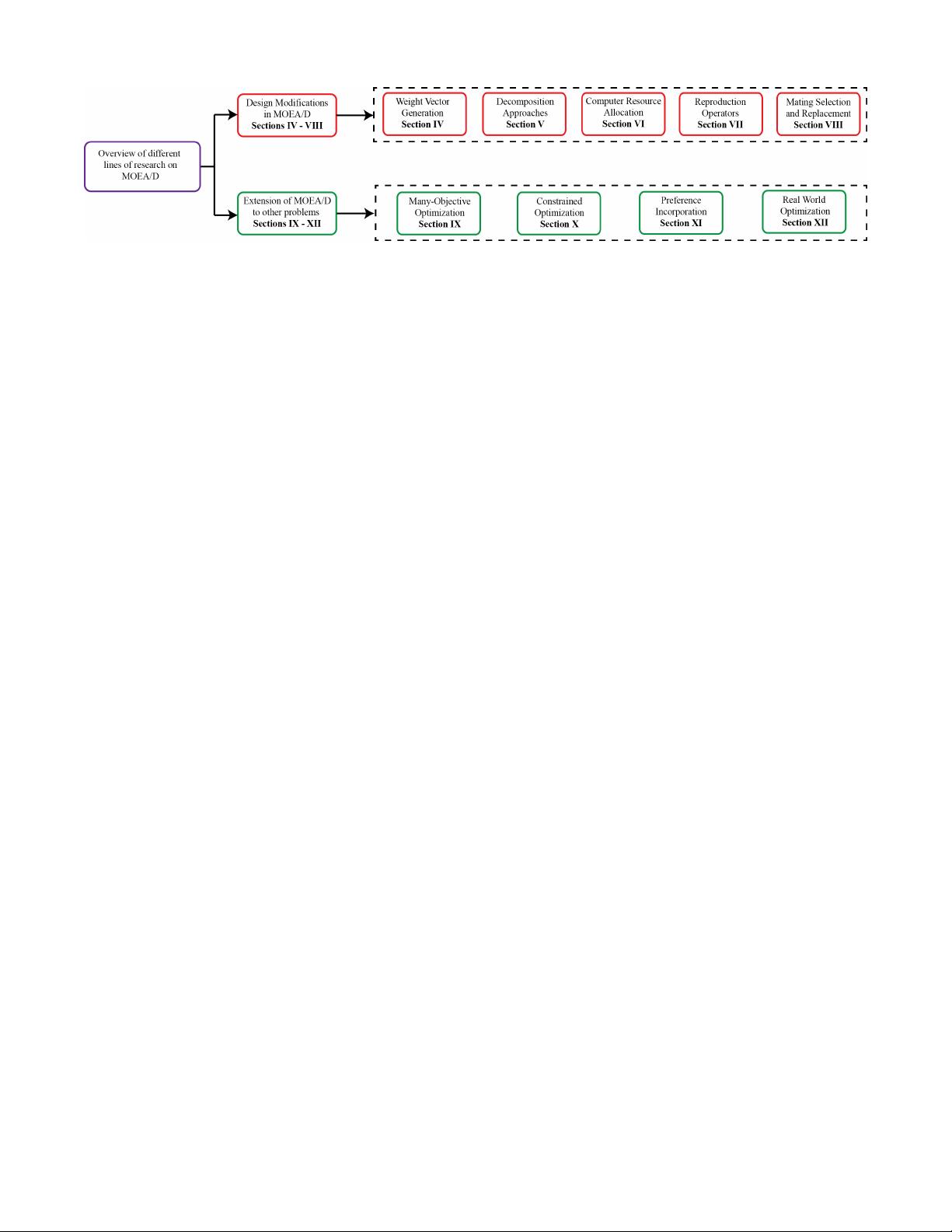
Fig. 1: Overview of different lines of research on MOEAs based on decomposition.

the search can be effectively focused within a small

area if the DM’s preference can be incorporated within

the evolutionary multi-objective optimization framework

[51]–[54]. Therefore, several studies have attempted to

integrate the preference of DM in decomposition-based

MOEAs, as discussed in Section XI.

• Application to Real World Optimization Problems:

The real world optimization problems are generally com-

plex and present a signiﬁcant challenge to the MOEAs,

which are often tested on numerical benchmark problems

only. Several studies have proposed MOEAs based on

decomposition to solve real world optimization problems,

as summarized in Section XII.

IV. STUDIES ON WEIGHT VECTOR GENERATION

METHODS

In MOEA/D framework, the choice of weight vector gen-

eration method is highly critical to the performance of the

algorithm. The original version of MOEA/D [9] and many of

its subsequent variants employ Das and Dennis’s [46] system-

atic approach, known as the simplex-lattice design method,

to generate evenly distributed weight vectors. However, in the

simplex-lattice design, the distribution of the weight vectors is

not very uniform for problem with 3 or more objectives [47].

Furthermore, in the simplex-lattice design [9], the population

size dramatically grows as the number of objectives increase

and the setting of population size is not ﬂexible [47]. Another

weight vector generation method widely employed in many

MOEA/D variants (such as MOEA/D-DRA [29]) is based on

uniform random sampling paradigm [19]. The advantage of the

uniform random sampling method over simplex-lattice design

is that the setting of population size is ﬂexible. This section

presents a review of the studies which have been undertaken

to develop novel weight vector generation methods.

In [55], Li et al. conducted a theoretical study on

decomposition-based MOEAs. In this study, the authors

proved to a certain extent that, in certain cases, polynomial-

sized evenly distributed weight vectors cannot map each point

in a polynomial-sized PF to a subproblem. Thus, the authors

highlighted the limitation of the simplex-lattice design method

and justiﬁed the various works in the literature which have

been dedicated to new methods for weight vector generation.

In [24], based on the geometric relationship between the

weight vectors and the corresponding optimal solutions under

the TCH approach, Qi et al. proposed a novel weight vector

initialization method, named WS transformation. The authors

illustrated that when the PF shape is close to the hyperplane

i=1

= 1, decomposition-based MOEAs should adopt

uniformly distributed solution mapping vectors that result from

WS transformation applied to uniformly distributed weight

vectors. A characteristic feature of the WS transformation is

that in the 2-dimensional objective space, the transformation

results in the same weight vector set except that the order

is reversed. Thus, the WS transformation is redundant in the

case of two-objective optimization problems. The experimental

study on 3-objective DTLZ1-DTLZ4 [56] problems (which

have simple PF shape) demonstrated that the WS transforma-

tion technique helps MOEA/D obtain much better uniformly

distributed P-O solutions

Tan et al. [47] proposed a new version of MOEA/D with

uniform design, termed UMOEA/D, for solving MaOPs. In

UMOEA/D, uniform design for experiment with mixtures

(UDEM) is employed to generate the weight vectors. With

UDEM, the weight vectors yield minimum discrepancy in

their distribution and thus the weight vectors are more uni-

formly distributed than the simplex lattice design employed in

MOEA/D. Furthermore, with UDEM, the population size is

not based on a formulaic setting and the population size N is

decoupled with the number of objectives m. The experimental

study on DTLZ1-DTLZ4 [56] test problems and two newly

proposed test problems (F1 and F2) having complicated PS

shapes, with 3-5 objectives, illustrated that UMOEA/D is

superior to MOEA/D [9] and NSGA-II [5], particularly for

higher dimensional problems and complicated PS shapes. In

addition, UMOEA/D is also found to signiﬁcantly outperform

state-of-the-art MOEAs on MOKP with 2-4 objectives.

Ma et al. [57] proposed MOEA/D with uniform decompo-

sition measurement, termed MOEA/D-UDM, to solve MaOPs.

MOEA/D-UDM is based on novel weight vector initialization

using uniform decomposition measurements. In MOEA/D-

UDM, the UDEM method employed in [47] is combined with

the simplex-lattice design to generate alternative weight vec-

tors and thereafter, the required number of weight vectors are

selected from the set of alternative weight vectors. MOEA/D-

UDM adopts the reverse Tchebycheff (rTCH) [36] decompo-

sition approach to construct scalar optimization subproblems.

The experimental study demonstrated that MOEA/D-UDM

signiﬁcantly outperforms MOEA/D [9] and UMOEA/D [47]

on DTLZ1-DTLZ4 [56] and WFG4-WFG9 [58] test problems

with 3-6 objectives.

In [25], Giagkiozis et al. presented a novel method for

weight vector generation, referred to as the generalized de-

剩余24页未读，继续阅读

阳光下的米雪

粉丝: 29
资源: 9

基于分解的进化多目标优化算法：MOEA/D综述

A Handbook Of Time-Series Analysis,Signal Processing And Dynamics.pdf

机器学习与智能通信.pdf

DeepLearningBook.pdf

2017.12 page394 Kotlin Blueprints-Packt Publishing(2017).pdf

基于深度学习和微表情检测的防疲劳驾驶检测综述.pdf

怎样修改MATLAB已有代码中数据-Ground-Plane-Polling:AkshayRangesh和MohanM.Trivedi，“道路

Kachru-Kallosh-Linde-Trivedi装置中的超对称抗D3叶片作用

Performance and Reliability Analysis Using Directed Acyclic Graphs - 1987 (10.1.1.380.4352)-计算机科学

Findkyhealthcare:findky.Healthcare

第九章 面板数据模型.doc

最新资源

第九章面板数据模型.doc