计算几何基础：点积与叉积的应用解析

"这个资源是一个关于计算几何的PPT课件，主要讲解了点、向量的概念以及如何利用点积和叉积进行几何问题的解决，包括判断向量的垂直和平行、点与直线的关系、线段相交的条件、求交点的方法，以及多边形面积的计算。此外，还提到了极角的概念及其在计算中的应用，以及处理浮点数精度问题的方法。" 在计算几何中，点和向量是基础概念。点通常表示位置，而向量则表示方向和大小。定义一个point类可以帮助我们存储和操作这些几何对象。点积（内积）和叉积（外积）是向量间的基本运算，它们在计算几何中扮演着重要角色。 点积计算公式为 `u·v = ||u|| * ||v|| * cosθ`，其中θ是向量u和v之间的夹角。当两个向量的点积为0时，它们互相垂直；反之，如果叉积为0，则它们平行。点积可以用于判断点是否在直线上，公式为 `cross(p-a, b-a) = 0`，其中p是点，a和b是直线上的两点。 叉积的结果是一个向量，其长度等于原向量构成的平行四边形的面积，方向垂直于这两个向量并遵循右手定则。它还可以用来判断线段是否相交，但需要注意端点是否包含在内。线段相交的条件可以通过点积和叉积的组合来确定。 直线的交点可以通过解线性方程组得到，例如 `(p1, v1)` 和 `(p2, v2)` 两条线的交点可以通过 `p = p1 + λv1 = p2 + μv2` 来找到，其中λ和μ是满足线性关系的参数。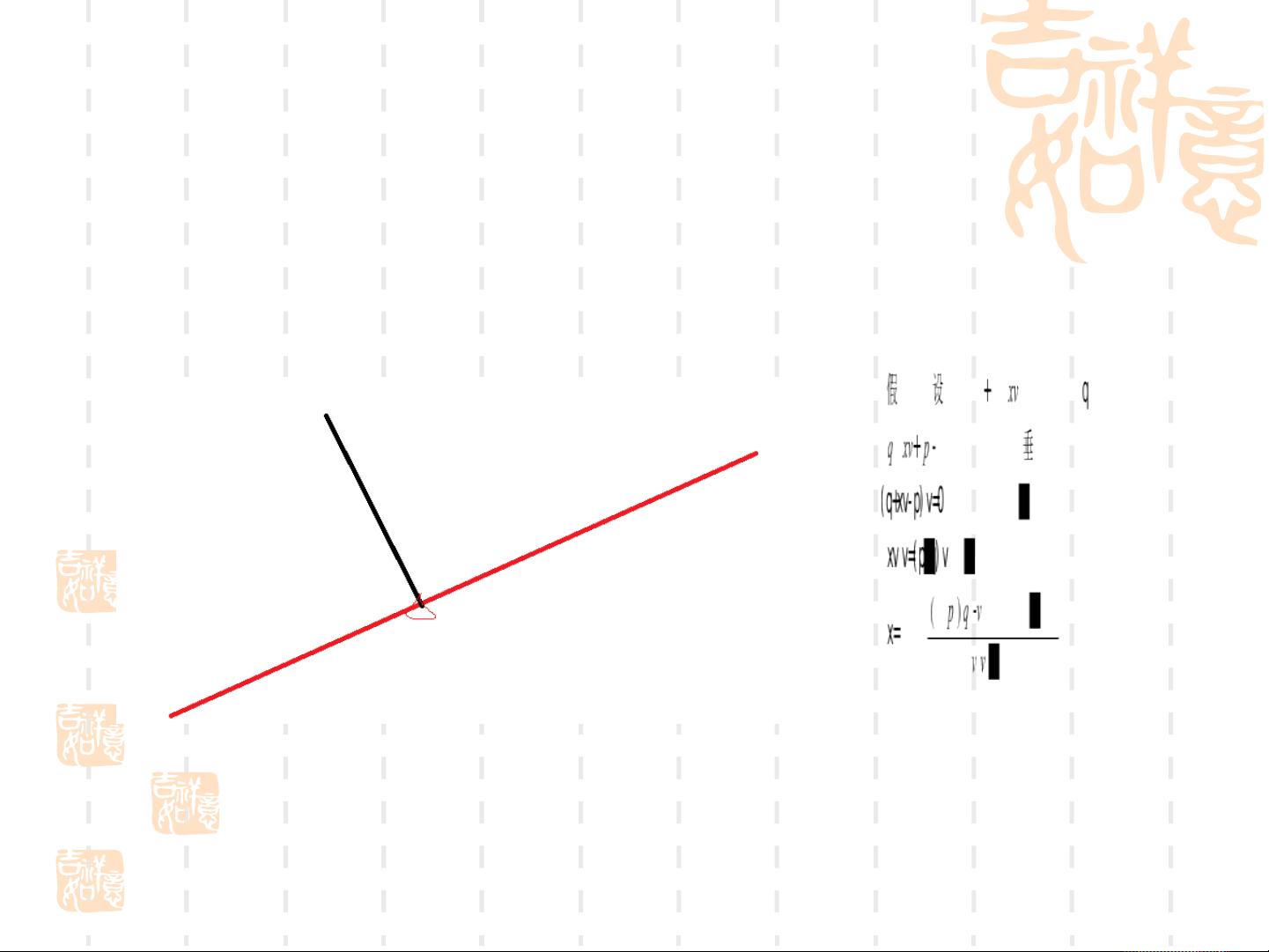 求一个点p垂直于线(q, v)的交点，可以设置点到直线的向量垂直于v，即 `(q + xv - p)·v = 0`，解这个方程可以得到交点的坐标x。 计算三角形的面积通常使用向量叉积，面积公式为 `S = 1/2 * |a × b|`，其中a和b是三角形的两边。对于凸多边形的面积，可以将多边形分割成若干个三角形，然后求和它们的面积。 极角（atan2(y, x)）函数在计算几何中用于获取精确的角度值，特别是在处理精度问题时，如防止由于浮点数精度误差导致的错误判断。在处理浮点数比较时，通常会设定一个较小的阈值（如eps），通过比较两个浮点数差的绝对值是否小于阈值来判断它们是否相等或近似相等。 这个PPT课件还提到了POJ2826题目，这可能是一个编程竞赛中的问题，具体细节未给出，但可以推断与计算几何的应用有关，可能是要求解决实际的几何计算问题。