一维与多维梯度下降详解：降低函数值的优化策略

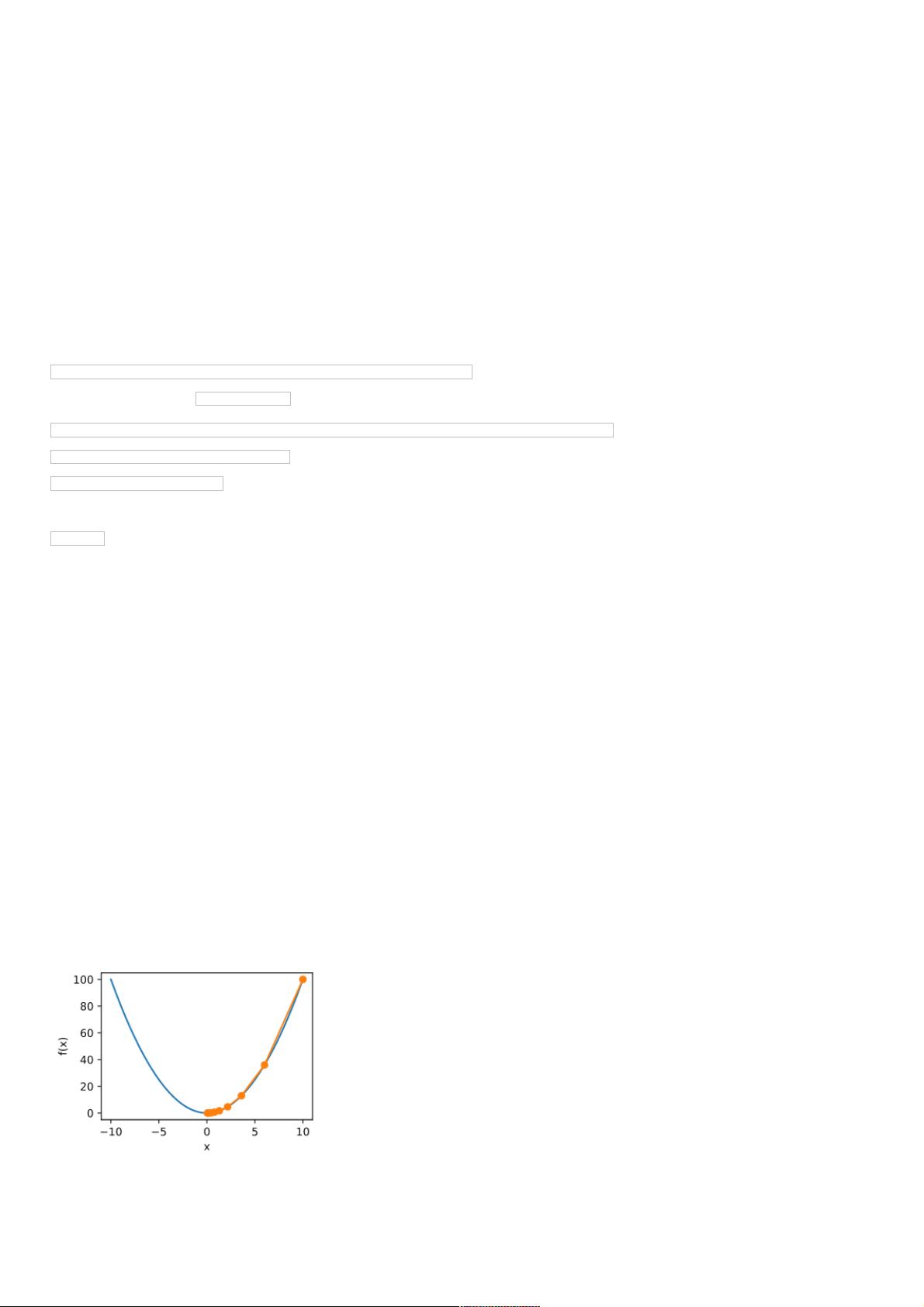
在"动手学深度学习(七) 梯度下降"这一章节中，我们深入探讨了梯度下降这一核心优化算法在深度学习中的应用。梯度下降是求解最小化或最大化的函数问题时，最常用的一种数值优化方法，它源自微积分的基本概念，尤其是泰勒级数展开。在这个教程中，作者通过Python的PyTorch库进行实例演示。 首先，一维梯度下降的原理是基于函数的梯度信息来调整参数。我们通过一个简单的例子来证明，沿着函数梯度的负方向移动自变量x，函数值会逐渐减小。例如，定义函数f(x) = x^2，其导数gradf(x) = 2x。函数gd(eta)使用固定的学习率eta，通过迭代更新x值，每次减去梯度乘以eta，如gd(0.2)所示，可以看到随着学习率的减小，函数在接近局部最小值处收敛得更慢，如gd(0.05)和gd(1.1)的结果对比。 接着，作者引入了局部极小值的概念，通过一个非线性函数f(x) = x * cos(c * x)，当初始学习率过大（如gd(2)）时，可能会导致算法陷入局部极小值而不是全局最小值。这表明在选择学习率时需要谨慎，因为它直接影响到搜索过程的效率和结果质量。 进一步，章节扩展到了多维梯度下降，这在处理具有多个输入变量的复杂模型时尤为关键。在多维空间中，梯度下降寻找的是函数值下降最快的方向，通常涉及到向量化的梯度计算和更新。这个过程可能涉及到梯度下降的变种，如批量梯度下降、随机梯度下降或动量梯度下降，它们分别考虑了所有数据点、单个数据点或结合过去梯度信息来改进更新策略。 总结来说，本章通过具体的代码示例和理论阐述，讲解了梯度下降的基本概念、一维和多维应用，以及学习率对优化过程的影响。对于理解深度学习模型的训练过程，特别是优化算法的选择和调整，这部分内容至关重要。掌握梯度下降算法不仅有助于提升模型性能，也是成为高效数据科学家的必备技能。