信号与系统基础：傅里叶变换与MATLAB实现

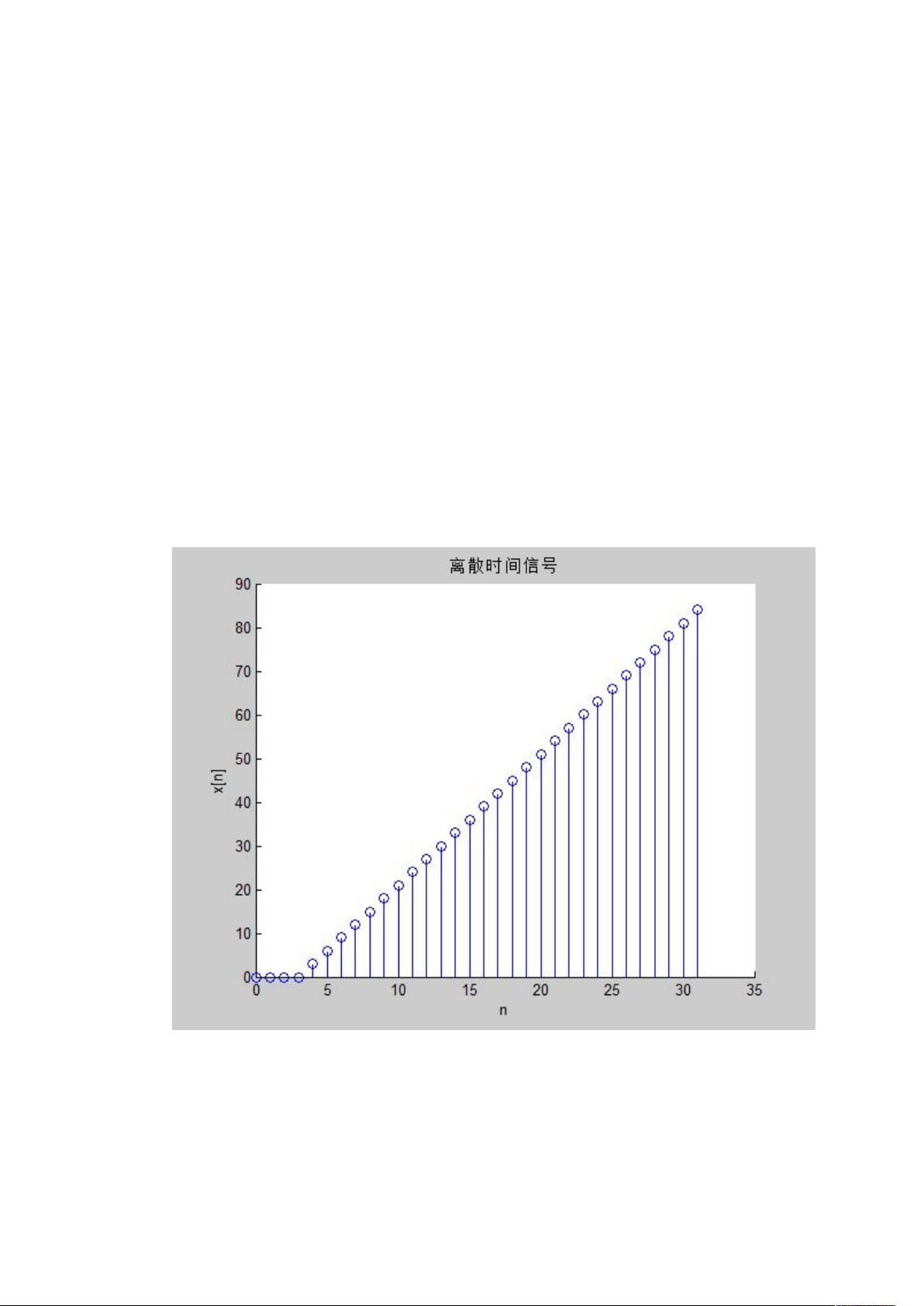
"这是关于信号与系统的一个初步总结，主要涵盖了连续时间和离散时间信号的定义、傅里叶变换的部分公式以及如何使用MATLAB进行信号的模拟。此外，还讨论了信号的能量与功率的计算方法，并提供了MATLAB代码示例。" 在信号与系统的研究中，我们首先要理解的是信号的基本类型。连续时间信号和离散时间信号是信号的两种基本形式。连续时间信号通常用函数x(t)表示，其自变量t是连续的，意味着信号在任意时间点都有定义。而离散时间信号则以x[n]的形式表示，自变量n只取一组特定的离散值，如整数序列。在MATLAB中，可以通过编写相应的脚本来创建这两种类型的信号。例如，文中展示了创建连续时间斜坡函数和离散时间斜坡序列的MATLAB代码。 傅里叶变换是信号分析中的核心工具，它将信号从时域转换到频域，揭示信号的频率成分。然而，具体公式未在描述中给出，但可以理解傅里叶变换对于理解信号的性质至关重要，特别是在滤波、调制和解调等应用中。 接着，我们讨论了信号的能量和功率。信号的能量E表示信号的总强度，对于离散时间信号，能量可以通过求和所有样本点的平方并取极限来获得；对于连续时间信号，能量则需要对信号的平方绝对值进行积分。平均功率P则为信号能量与时间的比值，反映了信号的平均强度。MATLAB代码示例展示了如何计算离散时间信号的能源和平均功率。 单位冲激函数δ(t)和单位阶跃函数u(t)是信号处理中的基础函数。单位冲激函数在所有时间点都为零，除了在t=0时，其值为无穷大，使得积分结果仍为有限值。单位阶跃函数则是一个在t<0时为0，在t>=0时为1的函数，常用于描述系统对输入信号的响应。 这些基础知识构成了信号与系统分析的基础。通过学习这些概念，我们可以更好地理解和处理各种通信系统、控制系统以及图像处理中的信号。后续的内容可能会进一步探讨傅里叶变换的性质、拉普拉斯变换、系统响应以及滤波器设计等主题。