Python实现PRO粒子群优化算法详解

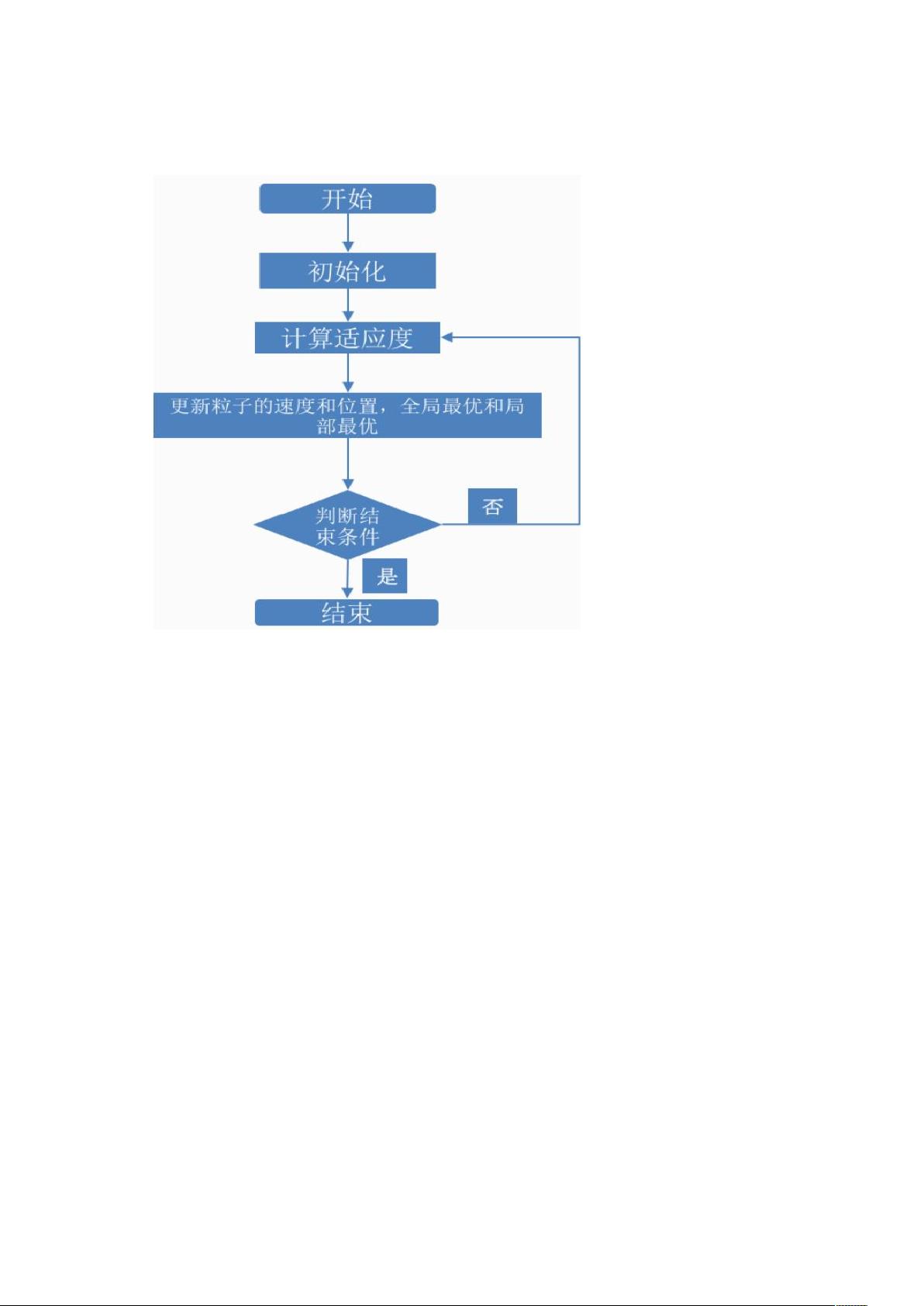
"本文将介绍PRO粒子群优化算法（Particle Swarm Optimization, PSO）的原理及其在Python中的实现。粒子群优化是一种基于群体智能的优化方法，它通过模拟鸟群寻找食物的行为来寻找问题的最优解。" 在PRO算法中，每个粒子具有四个关键属性： 1. **位置（Position）**：对应于问题的决策变量的值，即函数的自变量值。 2. **经验（Experience）**：即粒子经历过的最优解，相当于粒子自身的最佳位置。 3. **速度（Velocity）**：表示粒子在解空间中的变化率，决定了粒子在搜索空间中的移动方向和距离。 4. **适应度（Fitness）**：衡量粒子位置的优劣，通常由目标函数的值决定，值越小表示适应度越高。 算法流程如下： 1. **初始化**：首先，根据设定的粒子数量随机生成粒子的初始位置、经验（与初始位置相同）、速度（通常设为0）和适应度值。 2. **迭代更新**：在每一轮迭代中，粒子会根据以下公式更新速度和位置： - **速度更新公式**：`vi+1 = w * vi + c1 * rand1 * (pbesti - xi) + c2 * rand2 * (gbesti - xi)` 其中，`w`是惯性权重，`c1`和`c2`是学习因子，通常设置为2，`rand1`和`rand2`是0到1之间的随机数，`vi`和`xi`分别是当前速度和位置，`pbesti`是粒子的个人最佳位置，`gbesti`是全局最佳位置。 - **位置更新公式**：`xi = xi + vi+1` 这个公式用于确定粒子的新位置。 每个粒子的每个维度都需独立进行上述速度和位置的更新。 3. **适应度评估与更新**：在更新位置后，计算粒子的新适应度值，如果新适应度优于之前的经验（个人最佳位置），则更新经验。 4. **全局最优更新**：在整个种群中，如果发现有粒子的适应度优于当前全局最优，则更新全局最优位置。 5. **重复迭代**：直到满足停止条件（如达到最大迭代次数或适应度收敛等）。 以一个具体例子说明，例如求解函数 `f(x,y) = sqrt(x^2 + y^2) / sqrt(x^2 + y^2) + e^(cos(2πx) + cos(2πy)) - 2.71289` 的最优解，可以使用Python的matplotlib库创建三维图形，并应用PSO算法进行优化。这里省略了具体的Python代码实现，但通常会涉及到numpy库进行数值计算，以及matplotlib库进行结果可视化。 在实际应用中，PSO算法可以广泛应用于工程优化问题、机器学习参数调优、函数优化等领域。然而，其性能受到惯性权重、学习因子等参数选择的影响，需要根据具体问题进行调整。此外，为了防止早熟收敛，可以采用动态调整参数、引入混沌元素或者结合其他优化算法的方式改进PSO。