R语言实现时间序列分析：趋势平稳与MA模型

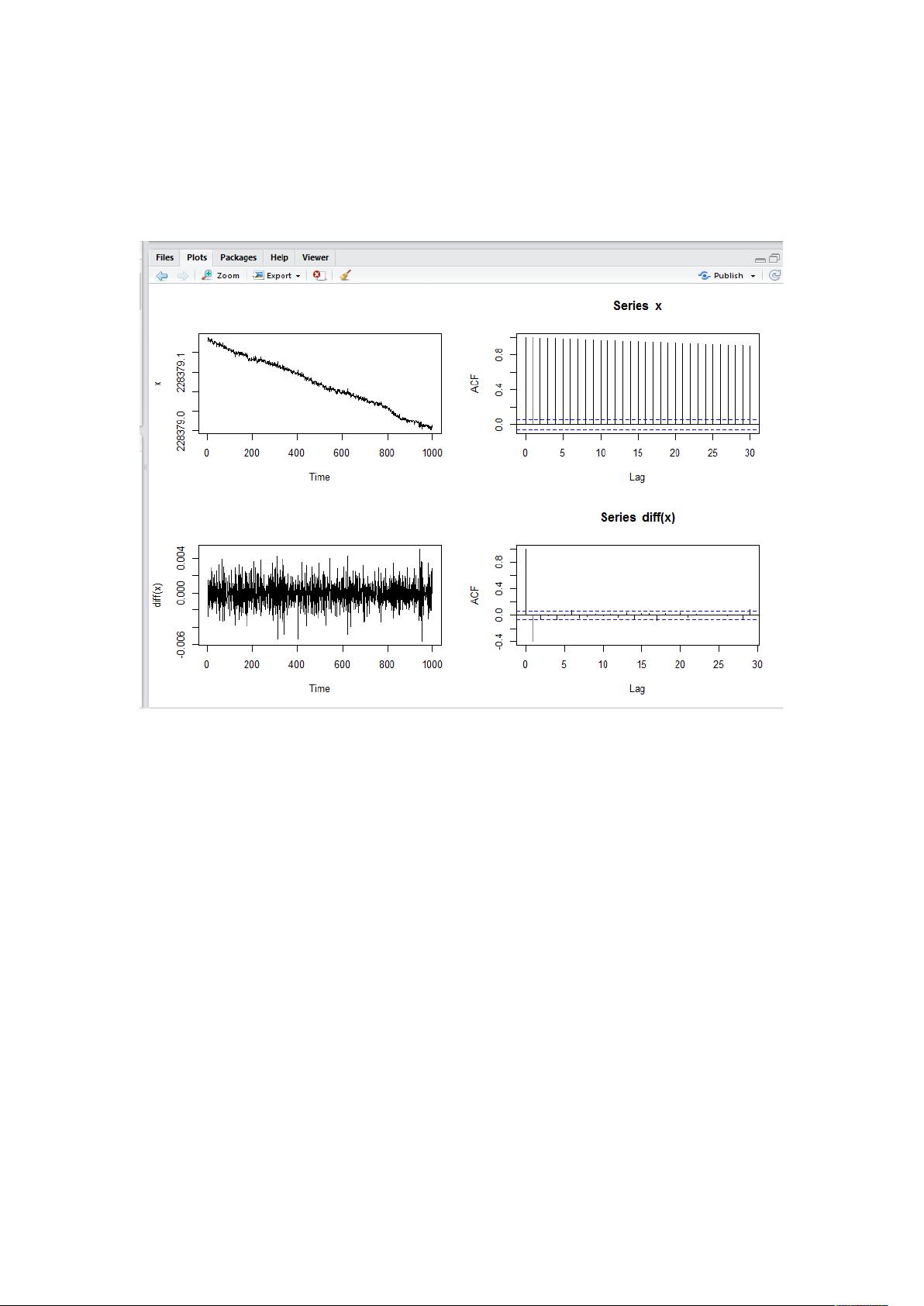
"R语言时间序列分析，包括趋势平稳过程和MA模型的探索。通过R语言的`scan`函数读取数据，使用`ts.plot`和`acf`函数进行趋势分析与差分处理，以及利用`arima.sim`构建不同参数的MA模型，并通过`acf`和`pacf`函数展示其自相关和偏自相关图。" 在统计学和数据分析领域，时间序列分析是一种常用的方法，用于研究和预测随时间变化的数据序列。R语言因其强大的统计功能和丰富的包库，成为了进行时间序列分析的理想工具。在这个案例中，我们将关注两个主要的时间序列模型：趋势平稳过程和移动平均（MA）模型。 1. **趋势平稳过程**： 时间序列分析的第一步通常是检查数据是否具有趋势或季节性。在R中，我们可以通过`ts.plot`函数绘制时间序列图，而`acf`函数则可以计算并显示自相关函数（ACF），帮助我们了解数据序列的内在结构。`diff`函数用于对数据进行差分，消除潜在的趋势。通过比较原始序列和一阶差分序列的ACF，我们可以判断数据是否趋向于平稳。如果一阶差分后的序列ACF衰减得更快，说明原序列可能是一阶单整的，即经过一次差分后达到平稳。 2. **MA模型**： 移动平均模型是时间序列分析中的重要组成部分，它假设当前观测值是过去一定期数的随机误差的线性组合。MA(2)模型意味着考虑了前两个滞后项的误差。在R中，`arima.sim`函数可以用来模拟不同参数的MA模型。例如，代码中模拟了三个MA(2)模型，分别是`theta[1]=0.5, theta[2]=0.3`，`theta[1]=0.5, theta[2]=-0.3`，以及`theta[1]=-0.75, theta[2]=-0.3`。通过`acf`函数绘制这些模型的ACF图，可以观察不同参数下的自相关性。同时，`pacf`函数用于绘制偏自相关函数（PACF），这有助于区分MA模型与其他模型（如AR模型）。 在示例中，MA模型的ACF图通常显示出明显的截尾模式，这是MA模型的一个特征。PACF则可以揭示模型的阶数，对于MA模型，PACF在达到某个滞后阶后应该快速衰减至零。 时间序列分析不仅限于趋势分析和建立模型，还包括模型选择、参数估计、预测等步骤。在R中，ARIMA（自回归积分滑动平均）模型经常被用作通用模型来捕捉时间序列的动态特性。`arima`函数可以帮助用户拟合和评估ARIMA模型，从而进行预测和建模任务。 总结，R语言提供了强大的工具来执行时间序列分析，包括检查数据的平稳性、构建和比较不同的时间序列模型。对于趋势平稳过程的理解和MA模型的运用，是进行有效时间序列预测的关键步骤。在实际应用中，还需要根据具体的数据特性和业务需求来灵活选择和调整模型。