低秩表示理论与应用：林宙辰北大演讲解析

" Low Rank Representation – Theories and Applications(ppt详解)" by 林宙辰,北京大学 这篇资料主要探讨了低秩表示的概念、理论分析、应用以及一些拓展。低秩分解是现代数据处理和机器学习领域的一个核心工具，特别是在大数据分析和矩阵理论中有着广泛的应用。以下是关于这一主题的详细解释： 1. **低秩表示** 低秩表示（Low Rank Representation）是指将高维数据通过一种方式表示成低秩矩阵的形式。这种表示方法能够捕捉数据的主要结构，通常用于降维和异常检测，因为正常模式往往在低维度下可以被有效描述，而异常则可能导致数据的秩增加。 2. **理论分析** - **稀疏表示**：数据点可以通过其他数据点的线性组合来表示，其中系数矩阵尽可能稀疏。这在信号处理和压缩感知中有重要应用。 - **稀疏子空间聚类（Sparse Subspace Clustering, SSC）**：公式(1)和(2)分别表示寻找最稀疏的系数矩阵来重构数据以及构建每个数据点的邻域表示。公式(3)和(4)则是优化问题，旨在找到低秩的Z矩阵，使数据矩阵X可以通过Z的乘积得到，同时保证Z的对角元素为零，以去除自相关。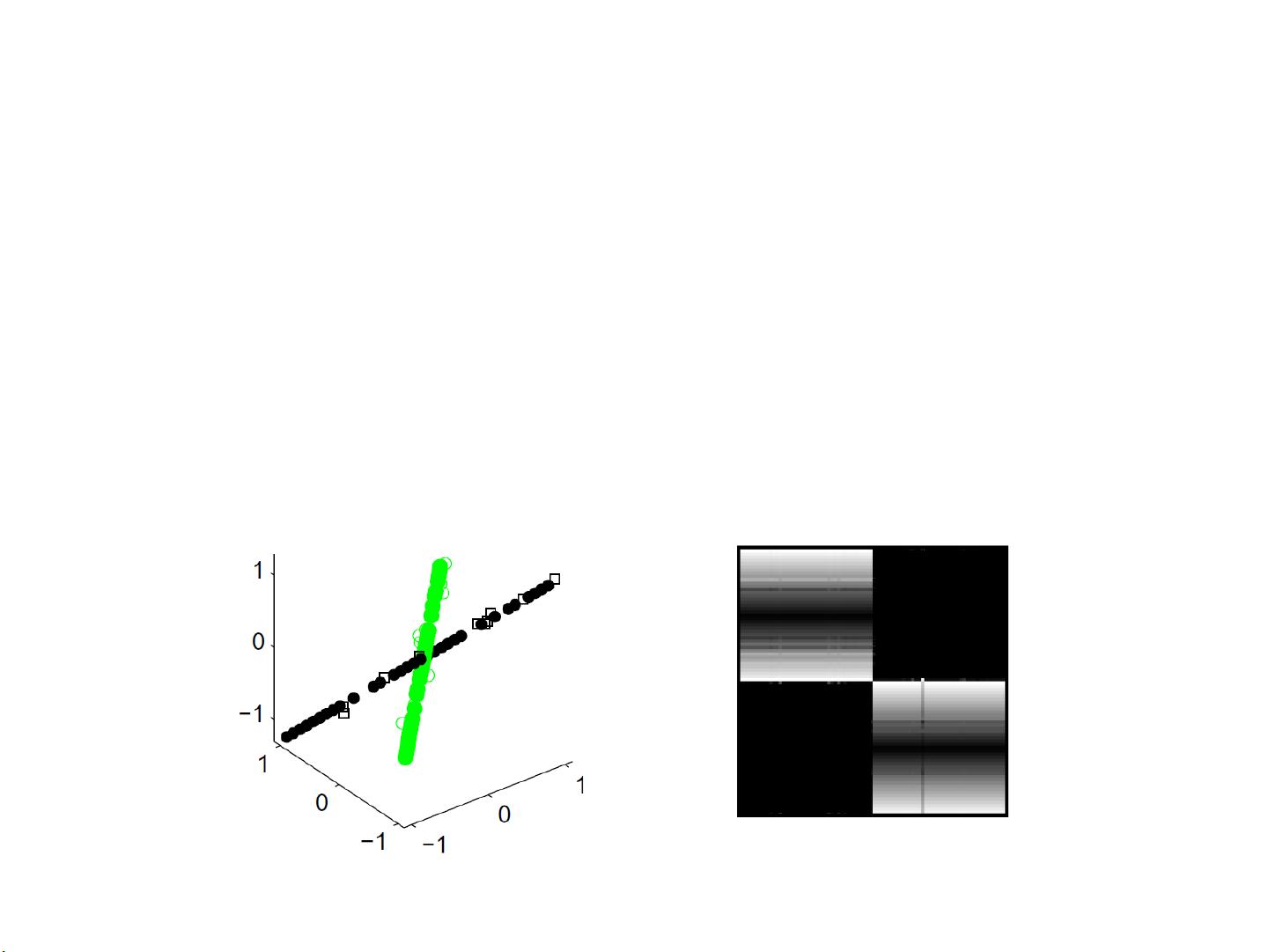 - **埃尔哈米法里和维达尔的工作**：他们在2009年的CVPR论文中提出了一种基于稀疏表示的子空间聚类方法，通过构建图并利用归一化切来进行聚类。他们证明，在理想情况下，即数据干净且独立于多个子空间时，Z矩阵会呈现块对角形式，每个块对应一个子空间。 3. **应用** - **数据聚类**：低秩表示常用于数据的无监督学习，特别是当数据集包含多个潜在的结构或子空间时，如图像分割、社交网络分析等。 - **图像恢复与压缩**：在图像处理中，低秩表示可以用于图像去噪和压缩，因为它能捕获图像的主要成分。 - **推荐系统**：在线上服务中，用户行为矩阵的低秩分解常用于推荐系统，以预测用户的兴趣。 4. **挑战与改进** - **噪声敏感性**：SSC对噪声非常敏感，没有内在的系数交叉验证机制来处理噪声或异常值。为了提高鲁棒性，后续的研究可能包括噪声模型的考虑或引入正则化项。 - **2D稀疏性**：2D稀疏性的概念可能提供关于如何改进低秩表示的线索，例如，通过结合不同维度的稀疏性来增强算法性能。 5. **一般化** 低秩表示的概念可以扩展到其他领域，例如通过结合其他约束（如非负矩阵分解）或使用深度学习框架来进一步提升模型的表现。 低秩表示是一个强大的工具，它在理论和实践中都发挥着关键作用。通过对数据进行低秩分解，我们可以揭示隐藏的结构，进行有效的降维，并解决各种实际问题。然而，理解其理论基础、克服实际应用中的挑战以及探索其更广泛的适用性，都是未来研究的重要方向。