使用多元线性回归分析广告投入与销售量关系

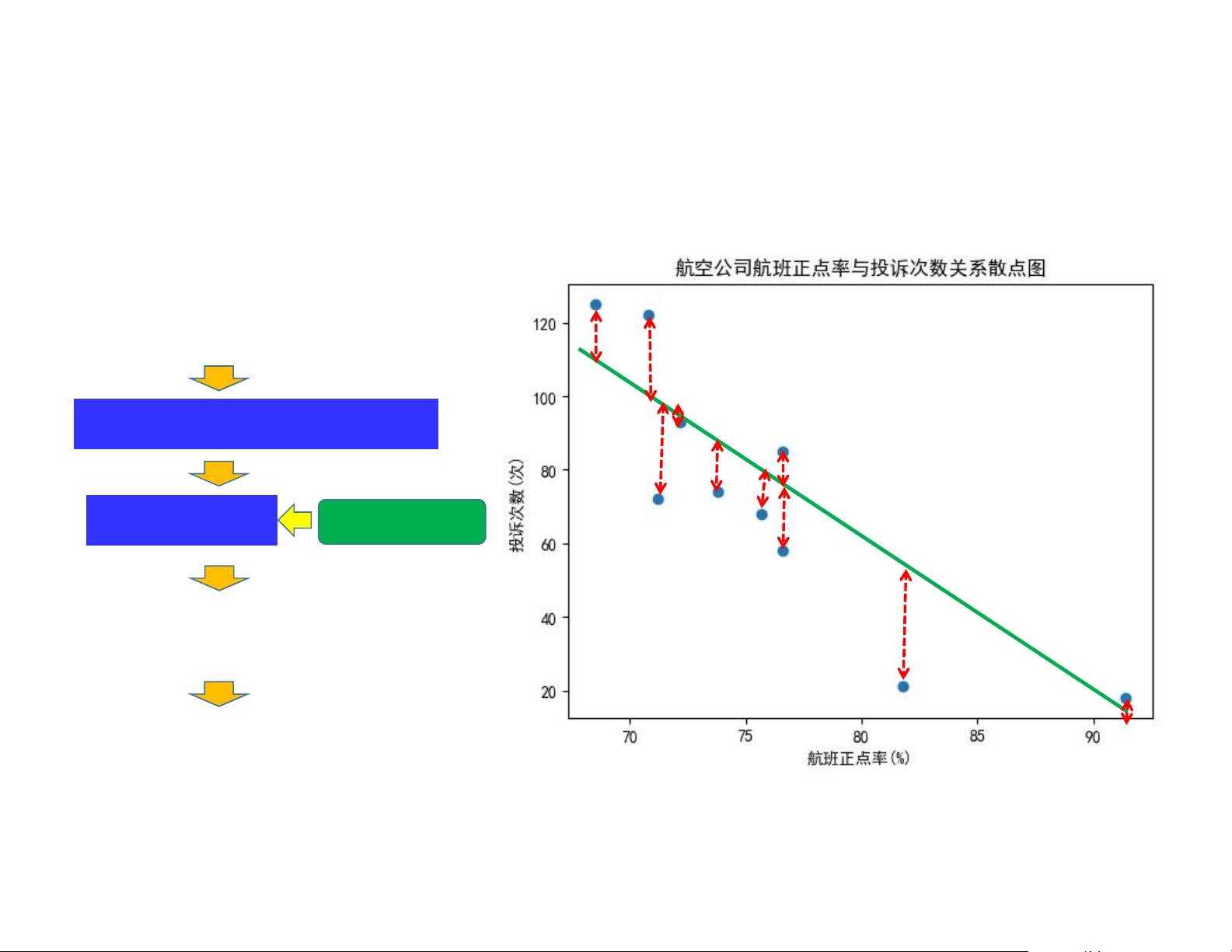
"该资源是一份关于多元线性回归的分析报告，主要探讨销售量与报纸、广播和电视三种广告投入之间的关系。通过200个样本数据进行研究，旨在理解广告投入对销量的影响，并利用多元线性回归模型进行预测。" 在商业环境中，了解广告投入对销售量的影响是至关重要的决策依据。多元线性回归是一种统计学方法，用于探究一个因变量（如销售量）与多个自变量（如广告投入）之间的关系。在这个案例中，自变量包括TV（电视广告）、Radio（广播广告）和Newspaper（报纸广告），因变量是Sales（销售量）。通过收集200个样本数据，我们可以构建一个多元线性回归模型来分析这些关系。 首先，我们需要对数据进行可视化，通常采用散点图展示销售量与各个广告投入之间的关系，以便初步观察是否存在线性关联。如果发现销售量与每个自变量的关系呈线性趋势，那么就适合建立多元线性回归模型。 多元线性回归模型的公式为 y = a1x1 + a2x2 + ... + anxn + b，其中y是因变量，x1, x2, ..., xn是自变量，a1, a2, ..., an是对应自变量的回归系数，b是截距项。回归系数表示自变量对因变量的影响程度，正负号则表示正相关或负相关。 为了找到最佳的回归系数，我们通常使用最小二乘法，即最小化误差（残差）的平方和，使得模型对数据的拟合度最高。这个过程可以通过数学优化算法，如梯度下降法或正规方程来实现。 在实际应用中，我们可以通过编程语言如Python来计算回归系数并构建模型。例如，根据给出的代码，得到的多元线性回归模型可以表示为：y = 0.04 * TV + 0.2 * Radio - 0.0028 * Newspaper + 2.99。这意味着每增加100元的电视广告投入，销售量预期增加0.04件；每增加100元的广播广告投入，销售量预期增加0.2件；而每增加100元的报纸广告投入，销售量预期减少0.0028件。 通过这个模型，公司决策层可以解答以下问题： 1. 哪种（哪些）广告渠道对销量影响最大？在这个例子中，广播广告的系数最大，所以它对销售量的影响最显著。 2. 当计划在TV、Radio、Newspaper渠道分别投入43.2、11.7、56.7百元时，可以预测销量大约为多少件？将这些数值代入模型，即可计算出预期的销售量。 多元线性回归是分析多个因素如何共同影响单一结果的有效工具。在这个特定案例中，它帮助公司理解不同广告渠道的投入如何影响销售量，并据此做出更明智的营销策略决策。