C语言数据结构：图论详解——存储、遍历与算法应用

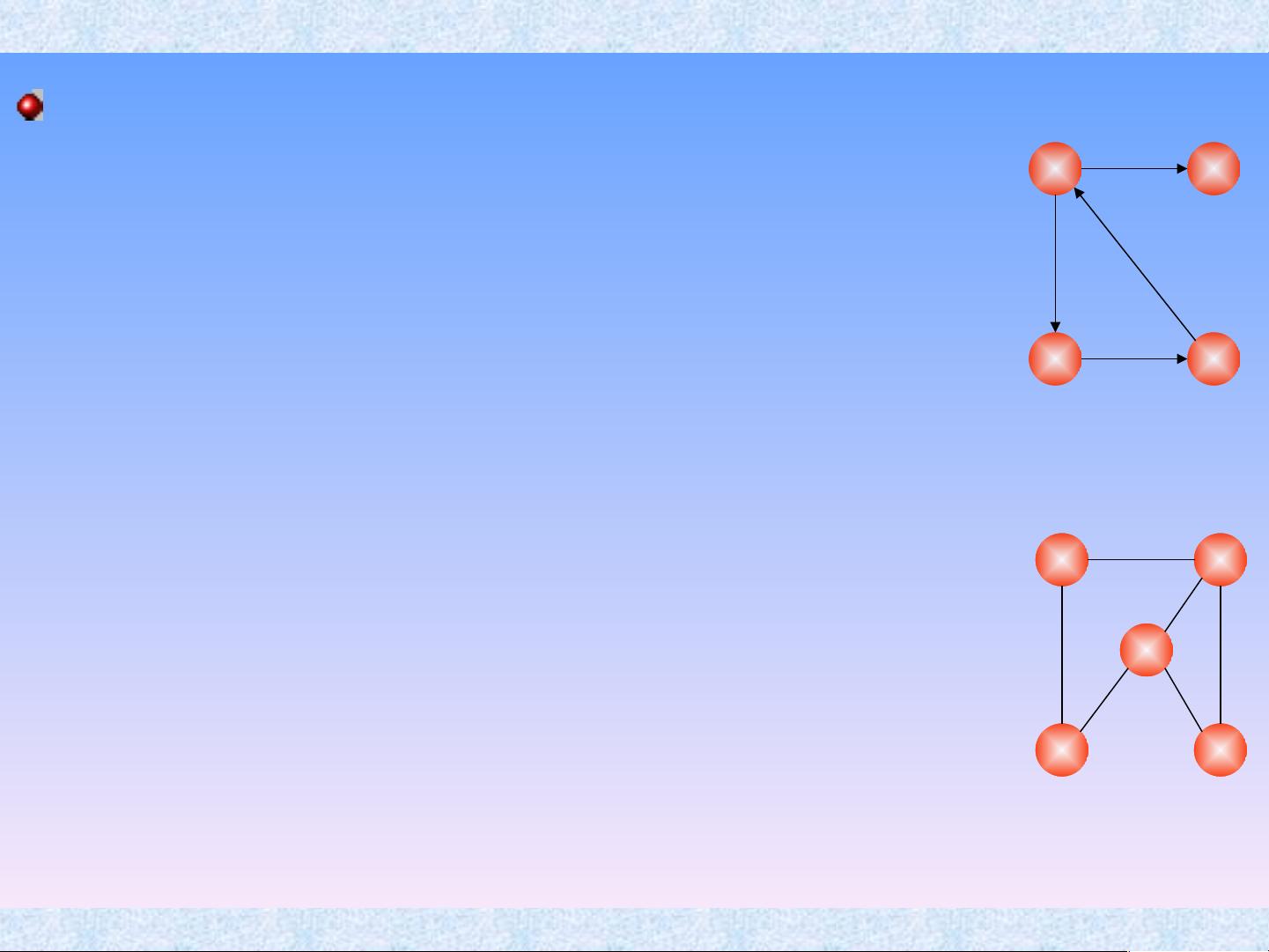
本资源主要关注的是数据结构在C语言中的应用，特别是关于图论部分。图是一种重要的数据结构，它在计算机科学中有广泛的应用，特别是在网络分析、路由算法、搜索引擎优化等领域。本章节详细探讨了以下几个核心知识点： 1. **图的基本概念**：图被定义为数据元素间存在多对多关系的数据结构，它由顶点集V和边集VR组成。顶点代表实体，边则表示实体间的关联，可能是无方向的（边）或有方向的（弧）。 2. **图的存储结构**： - **邻接矩阵**：用于表示图的二维数组，通过行和列来存储顶点之间的连接情况，效率适合稠密图。 - **邻接表**：一种稀疏图的存储方式，通过链表或数组实现，每个顶点链接到其相邻顶点的列表，节省空间。 - **有向图的十字邻接表**：特别适用于有向图，用两个列表分别存储出度和入度信息。 3. **图的遍历**： - **深度优先搜索（DFS）**：从一个顶点开始，尽可能深地搜索分支，直到无法继续为止，再回溯寻找其他路径。 - **广度优先搜索（BFS）**：按照层级顺序遍历图，从起点开始，先访问最近的顶点，再逐渐扩展到更远的节点。 4. **最小生成树**： - **Kruskal算法**：贪心策略，通过不断加入边来构建树，直至所有顶点连通，不形成环。 - **Prim算法**：从一个顶点开始，每次选择与当前树相连的最短边，逐步扩展树直到覆盖所有顶点。 5. **最短路径**： - **Dijkstra算法**：用于单源最短路径问题，每次选择未访问的最短边进行扩展。 - **Floyd算法（Warshall-Floyd算法）**：用于求解所有顶点对之间的最短路径，适合稠密图。 6. **AOV网络与拓扑排序**： - AOV（活动-结点-边）网络用于描述活动、执行这些活动的结点以及它们之间的依赖关系，拓扑排序是活动顺序的一种排列方法。 7. **AOE网络与关键路径**： - AOE（活动-结点-事件）网络，用于项目管理，关键路径是指决定项目完成时间的最长路径。找到关键路径有助于确定项目的最早开始时间和最晚结束时间。 此外，教材还涉及到了图的一些基本操作，如创建和销毁图结构，定位顶点、获取顶点值、查找邻接顶点等，这些都是实现图算法的重要步骤。这些知识点在处理实际问题时，能够帮助理解和解决复杂的网络结构问题，是计算机科学特别是算法设计中不可或缺的一部分。