分治算法实践：循环赛日程表安排与最近点对问题

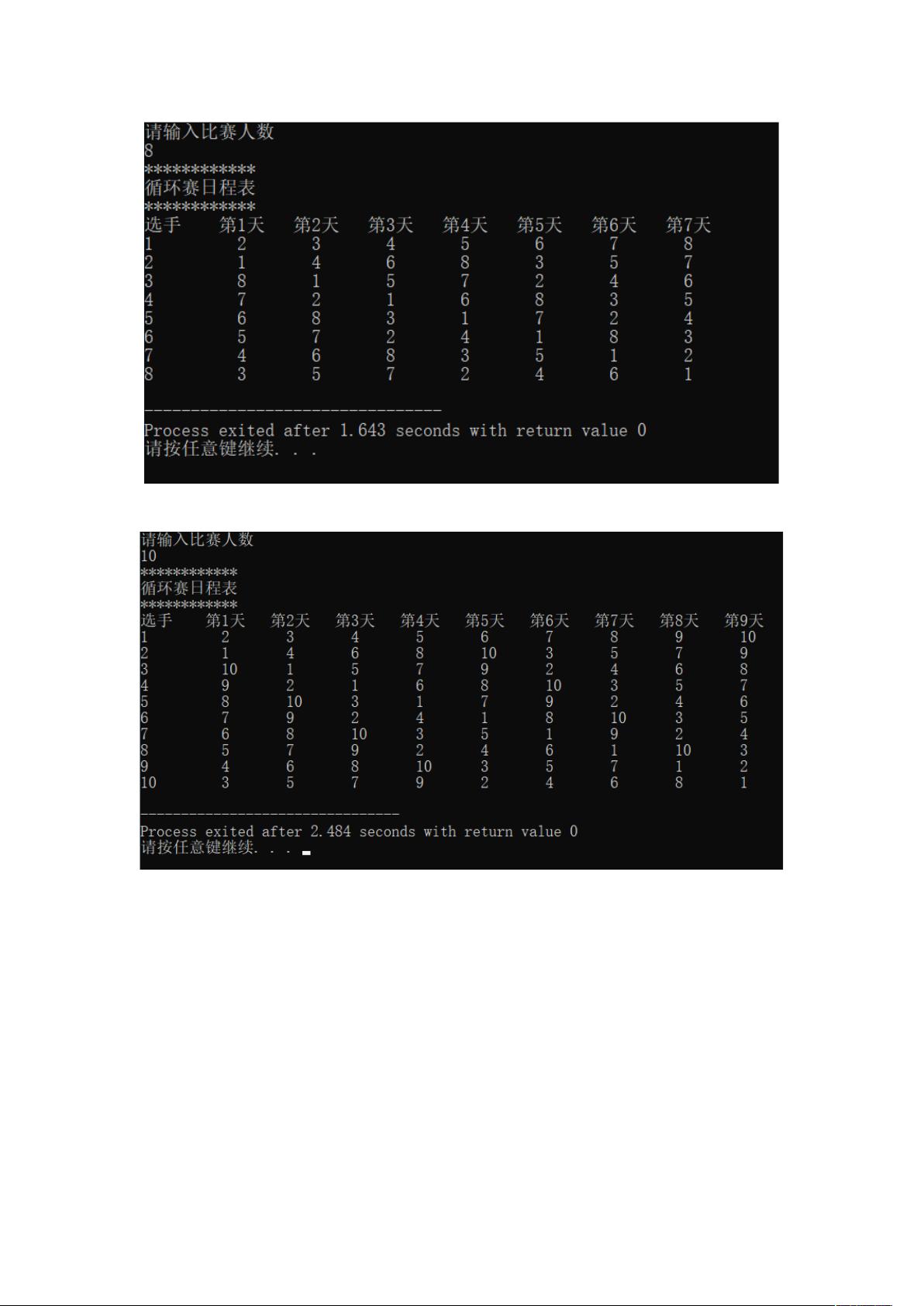
"实验一涉及递归与分治策略，主要涵盖了两个问题：循环赛日程表安排和最近点对问题。实验旨在让学生深入理解分治算法和蛮力法的原理，提高编程实现这些算法的能力，并通过递归方法解决相应问题。在循环赛日程表安排中，使用了多边形轮转法实现；而在最近点对问题中，要求用分治和蛮力法分别解决，并分析时间复杂性。" **循环赛日程表安排**： 在循环赛日程表安排问题中，通常涉及到的是n个参赛者之间两两对决的情况。分治算法在此问题中的应用是通过将问题分解为更小的子问题来解决。多边形轮转法是一种典型的分治策略，它将选手分为两半，然后通过轮转的方式安排比赛。这种方法适用于奇数和偶数人数的情况。程序代码中，`lunzhuan`函数实现了这个过程，首先根据人数判断是奇数还是偶数，然后通过循环填充比赛日程矩阵`plan`。通过递归调用，可以有效地处理不同规模的参赛者数量。 **最近点对问题**： 最近点对问题是计算几何中的一道经典问题，目标是在给定的一组二维点中找到距离最近的点对。分治算法通常通过将空间划分为四个象限，递归地解决问题。而蛮力法则通过简单地比较每对点之间的距离来找到最小值，其时间复杂度为O(n^2)。实验要求学生对比分治法和蛮力法在处理随机生成的100点对时的时间效率，从而理解两种方法的时间复杂性差异。 **分治算法**： 分治算法是一种解决问题的策略，将大问题分解成若干个规模较小、相互独立、与原问题形式相同的子问题，再将子问题的解组合得到原问题的解。这种方法常用于排序、查找、计算几何等领域，如归并排序、快速排序和二分查找等。 **递归**： 递归是编程中一种重要的技术，它是指函数或过程在执行过程中调用自身的行为。递归可以简化问题的描述，使代码更加简洁易懂。在解决循环赛日程表安排问题时，递归使得算法能够自底向上地处理各个子问题，直到问题规模减小到可以直接解决。 实验通过这两个问题的实践，旨在让学生掌握递归和分治的思想，提升算法设计能力，同时理解不同算法在解决实际问题时的时间复杂性特点。